From Euclid to Euler to Einstein

It is of course the holiday tradition this time of year, to exchange gifts and ponder over how you would explain modern mathematics to the ancient Greeks.

In line with the latter part of that tradition, I’ve been sketching out a diagram to explain Euler’s number $e$ (2.71828…) to Euclid. It turns out that even though the classic Greek mathematicians knew all about the number π (3.1415…), they never knew about or defined the number $e$. Which is a shame, because they could have. And had they done so, they could have beaten Einstein to the punch 2500 years earlier.

Just a quick note here: for those of you who have not heard of $e$, it pops up all over the place in science, and especially when things are growing or accelerating. For example, suppose you just crossed the state line, and for some reason you thought that the mile-markers were actually speed limits, so that at the one-mile marker you slowed down to go at one mile an hour, and so on. Suppose that there were a lot of mile markers along the way, and so you were continuously speeding up with each marker. Obviously you would be going pretty slow, but at least you are speeding up. It turns out that if you obeyed the signs to the letter, by the end of one hour from mile marker one you will be at the $e$ mile marker, and would be going $e$ miles an hour.

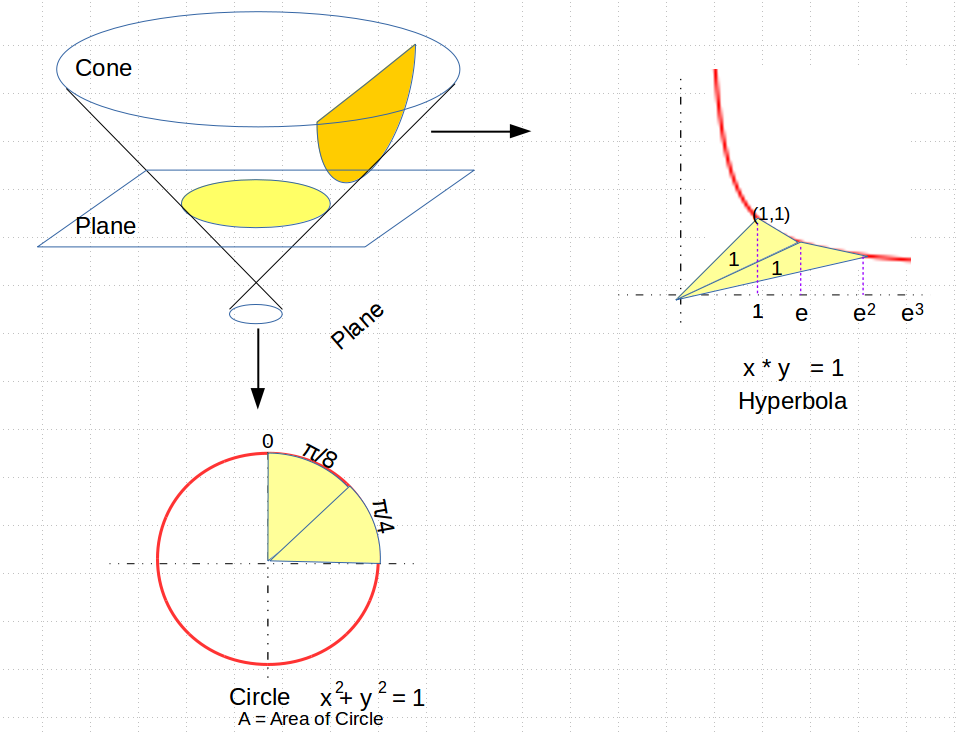
In any case, after much fiddling around and fanfare, here is the diagram I came up with that I think would make Euclid happy. It is a “proof without narrative”, and simply uses the classically understood conic sections (e.g. circles, and hyperbolas) to show how the numbers π and $e$ may be used to relate areas of pie-shaped sectors in two conic sections, to the linear measurements along their respective curves:

One of the things I like about this diagram is that on the one hand it shows how these two numbers are similar, in that they both provide a ratio relating the area of a sector in each type of conic section, with a linear measure, but on the other, we see how these two numbers differ in a fundamental way with successive sectors.

For circles of radius 1, its area compares with its radius squared by a ratio of π (so the pie-slices are each π/8). For the hyperbola, drawing a line from the center to the vertex of the hyperbola, a sector of area one is made by drawing a second line whose x-axis length differs from the area by a ratio of $e$. In both cases we have a ratio relating a linear measure to an area.

But at this point the similarity ends. For as we go to successive circular arcs, the areas remain in fixed linear ratios, so to produce a quarter of a circle, you have an arc-length of π/4, and so on. But for the hyperbola, to produce a sector of area 2, you need to draw a line segments whose x-axis length is not $2 * e$, but $e$ to the power of 2, in other words $e^2$. For an area of three, you need to use $e^3$, and so on.

So what we see is that the number π seems to be most commonly used as a linear factor or ratio, having to do with rotational symmetry in space, while the number $e$ seems to be used as the base of an exponent, and is involved with things that grow exponentially over time.

Which brings us to light, waves, and Einstein’s space-time.

What do cones, planes and conic sections have to do with spacetime? Suppose you turn a flashlight on and off quickly. The light pulse from that event travels out in all directions at the same speed, $c$, the speed of light. Einstein (and Minkowski) suggested that we view the event where time plays the role of a fourth dimension. If we toss out one of our three dimensions, and make the time dimension the z-axis, we can visualize the light propagating out.

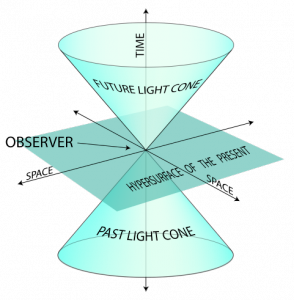
So in the picture on the right, the horizontal plane represents space at time $t=0$, and the vertical dimension is time, with the “up” direction representing the future, and “down” representing the past. The flashlight has just gone off at time zero, but now the light wave is expanding out in a circle, getting larger with time. And so as it grows over (upward) time, the expanding circular wave traces out the “future light cone”. Conversely, all of the light from the past that reaches us can only come from the region below the plane, marked by the “past light cone”.

The thing to note is that these “space-like” planes are always horizontal, though they may tilt a little due to relativistic motion of the observer. Space-like planes can be identified by the fact that their “normal” line (the one perpendicular to the plane) are pointing roughly up, in a time-like direction. Space-like planes can only intersect light-cones in circles or ellipses. In no case can an observer’s “plane” ever become vertical, so that its normal vector is pointing in a space-like direction outside of the light cone. Such planes are called “time-like”, and have the property that they always intersect light cones in hyperbolas.

So I am hoping that you are starting to see how I think these two numbers $pi$ and $e$ are related, but also very different. Somehow, the number $pi$ is related more to space, and to circular rotation in space, while $e$ seems to be related to time, hyperbolic curves, and exponential growth over time.

It turns out that we can even be very specific about how $e$ and $pi$ are related to each other, but it requires the introduction of a number that the ancient Greeks would have no concept of, and that is the number $i$, the square root of negative one.

The relationship was itself discovered by Euler himself, and has come to be known as Euler’s Equation, and has also been called (at least by mathematicians), The Most Beautiful Equation in the World. I hope some time in a future post to try to explain what the equation means, but for the moment, we will just display it here and be done with it.

$$ e^{i\pi} + 1 = 0  $$

And yes, this is how I spend my holiday vacations. Having Fun ! Happy new year !