A Chess Puzzle, Part VII Episode 1: The Fractal Queen

Part VII Episode 1 of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

We have now come to the final (two-part) chapter of this two year journey, exploring the maximum “density” of various chess pieces on an infinite chess board, with the rule that no piece is attacking any other. The journey has taken us through many realms of mathematics, including geometry, set theory, group theory, differential calculus, real analysis, combinatorics, topology, measure theory, and transfinite numbers.

With that exhaustive list of mathematics, one would think that our last chess piece —- the Queen —- would have little more to offer us. After all, in terms of attacks, the queen is simply a Rook that can also attack like a Bishop, and so any position of “friendly” queens is also a position of friendly rooks and/or Bishops. In terms of set theory, the set of unguarded queen positions on a board is the intersection of unguarded Bishop and Rook positions.

But as we shall see, the Queen takes us on one final trip, through some of the deepest mathematics that we have yet encountered.

Unguarded Queens on the Countable Board

There is one catch with the finite $N \times N$ board $B_N$, which is that while a maximal unguarded Rook  position consists of $N$ rooks, a maximal unguarded Bishop position will have $2N-2$ bishops, and so (on the finite boards at least) maximal unguarded queen solutions will not be maximal as bishops, merely “Rook maximal” (to coin a phrase).

There is a simple way in which one can take finite solutions to the unguarded queen problem and turn them into solutions on larger boards, and by extension to the countably infinite board $B_\omega$. We we show one such construction here.

For example, let’s start with a solution to the unguarded Queen problem on the 5-board $B_5$:

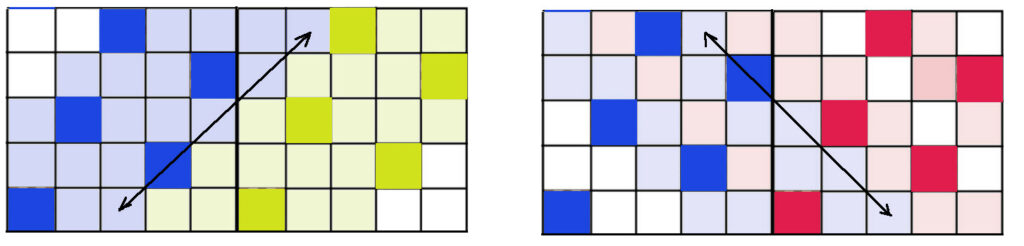
If we now go to the 25-board $B_{25}$, we can think of it as a $5 \times 5$ array of $B_5$ boards. So suppose we place one of the above solutions on each of the array locations corresponding to the queen solutions, like this:

it turns out that this is a Rook-maximal unguarded Queen position on the 25 board. It is not obvious that it is an unguarded Bishop position; even though it is clearly an unguarded rook position you have to verify that none of the queens in one block attack diagonally any other queens in the other blocks. Amazingly, none of them do. To see this, we only have to consider the diagonal attacks between the “blocks” of queens. As can be seen, when two such blocks are placed adjacent to each other, the queens in each block control separate diagonals from the other block:

In the exact same manner one can take this solution on $B_{25}$ and place five copies on a $B_{125}$ board to produce an unguarded queen solution there, and continue in with all larger boards that are powers of 5.

One can then extend this generally to the countably infinite board  $B_{\omega}$ by simply noting that each finite solution $Q_i$ contains all smaller solutions, and so you can simply take the union of all of them to cover $B_{\omega}$, that is. our position $Q_{\omega}$  is given by:

$$Q_{\omega} = \bigcup^{\infty}_{i=0} Q_i$$

To make this infinite solution explicit, we need to give for each horizontal integer coordinate $x = \{0,1,2 …\}$ the vertical location $y = \phi(x)$ where the queen in that column is located. There is a neat trick for doing this. We first explictly define the first five $y$ values of $\phi$ from $x=0$ to $x=4$:
$$\begin{cases}
\phi(0) = 0 \\
\phi(1) = 2 \\
\phi(2) = 4 \\
\phi(3) = 1 \\
\phi(4) = 3 \\
\end{cases}\tag{PHI}
$$
Note that $\phi$ is a permutation of the five digits $\{0,1,2,3,4\}$. We then define $\phi(x)$ for all other positive integers $x$ by writing its value in base 5, ie,
$$x_5 = d_1 d_2 … d_n,$$
where $d_i$ are base 5 digits, and then define
$$\phi(x)_5 = \phi(d_1) \phi(d_2) … \phi(d_n)$$
That is, we permute each of the input digits of $x$ by $\phi$ to get the base 5 representation of the output $y$. Note that this also shows that all rows contain a queen, because to find the column $x$ where a queen resides on row $y$, just write $y$ in base 5 and apply the inverse of $\phi$ on the digits to get $x$.

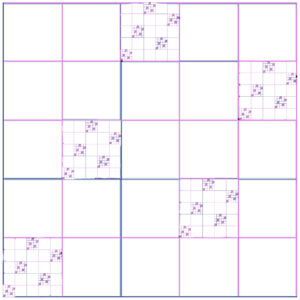
A close approximation of the infinite board $B_{\omega}$ solution can be seen below, with a scaled down version of the solution on the very large board $B_{625}$:

We should remark here that there is nothing magical about the number 5. We could just as easily have found another solution for the omega board using a $7 \times 7$ board queen solution as a template, such as this:

However, this approach does not always work. Not all 7-board solutions work for example, and no queen solutions on the 4-board work:

The Troublesome Transfinite Queen

As with the Rook and Bishop, we now turn to unguarded queen problem on the board of the continuum $B_c$. Unlike the omega board whose “squares” are located at integer coordinate 0,1,2…, this board is transfinite, and has an uncountably infinite number of “squares” whose coordinates are real numbers. As with the Rook and Bishop, we will look strictly at the open bounded case where the board is the unit square (technically, that would be $B_I$, where $I$ is the open unit interval $I = (0,1) = \{ x: 0 \lt x\lt 1\} $. We have selected the open interval to eliminate the corner points and boundary.

As a naïve first attempt at constructing a solution, we might try the same trick as above, with an iterative process. The difference here, however, is that instead of a union of successively larger sets of discrete queens on the integer board, we create an infinite sequence of shrinking compact nested sets $Q_i, i=0,1,2,…$ where $Q_0 \supset Q_1 \supset Q_2  … $ and whose intersection forms the solution $Q$, that is,

$$Q = \bigcap^{\infty}_{i=0} Q_i$$

The first three iterations are shown below:


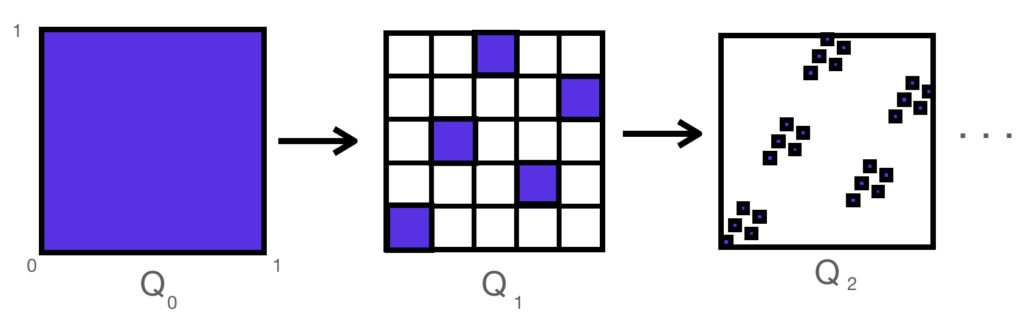
And the resulting fractal set $Q$ looks very much like the board $B_{625}$ shown above. It can be shown that this set has a fractal dimension of 1, and a 1-dimension fractal measure of $\sqrt 2$

Now one would think that this “solution” $Q$ works, because at each iteration the cells do not “attack” each other as Queens. However, the actual “squares” on this transfinite board are points, so we need to make sure that there are no collisions in he limiting case.

Failure!

… In fact, the solution $Q$ we have constructed is a failure.

Let’s first try to characterize the point set $Q$ mathematically, as we did in the case of the omega board.

In the omega board, whose squares had integer coordinates going off to infinity, we represented the values in Base 5, that is, multiples of powers of 5. In the case of the unit square, all coordinates are real numbers between 0 and 1, and we are dividing them by powers of 5.

We have the following theorem:

THEOREM: a point $(x,y) \in B_c$ is in $Q$ if and only if $x$ can be expressed as a Base 5 decimal, ie

$$x_5 = 0.d_1d_2d_3 ….$$

in such a way that the value $y$ can be expressed in Base 5 as

$$y_5 =0.\phi(d_1)\phi(d_2)\phi(d_3) …$$

And $\phi$ is the permutation on the digits $\{0,1,2,3,4\}$ defined by equation (PHI).

PROOF: The proof consists of observing that on the $nth$ iterative step $Q_n$ the points $(x,y)$ which are removed are exactly those where in their Base 5 representation the $nth$ digit of $y$ is not equal to $\phi(d_n)$. Conversely, if the $\phi()$ relationship holds for all digits of $x$ and $y$, then no iteration of $Q_n$ will eliminate the point $(x,y)$. QED

So if this is all good, what is the problem?

The problem is, there are many real numbers which can be expressed as infinite Base 5 decimals in two ways. In fact, any number whose Base 5 expansion terminates (ie, ends with 000…) has this property. For example, the (Base 10) value $x=0.2$ can be expressed (in Base 5) as either

$$x_5 = 0.100000000….$$

or

$$x_5 = 0.044444444….$$

(In the same way that in base ten 0.9999… = 1).

But if we apply $\phi()$ to these two decimal expansions we get two distinct values for $y$, ie

$$y_5 = 0.200000…$$

and

$$y_5 = 0.0333333…$$

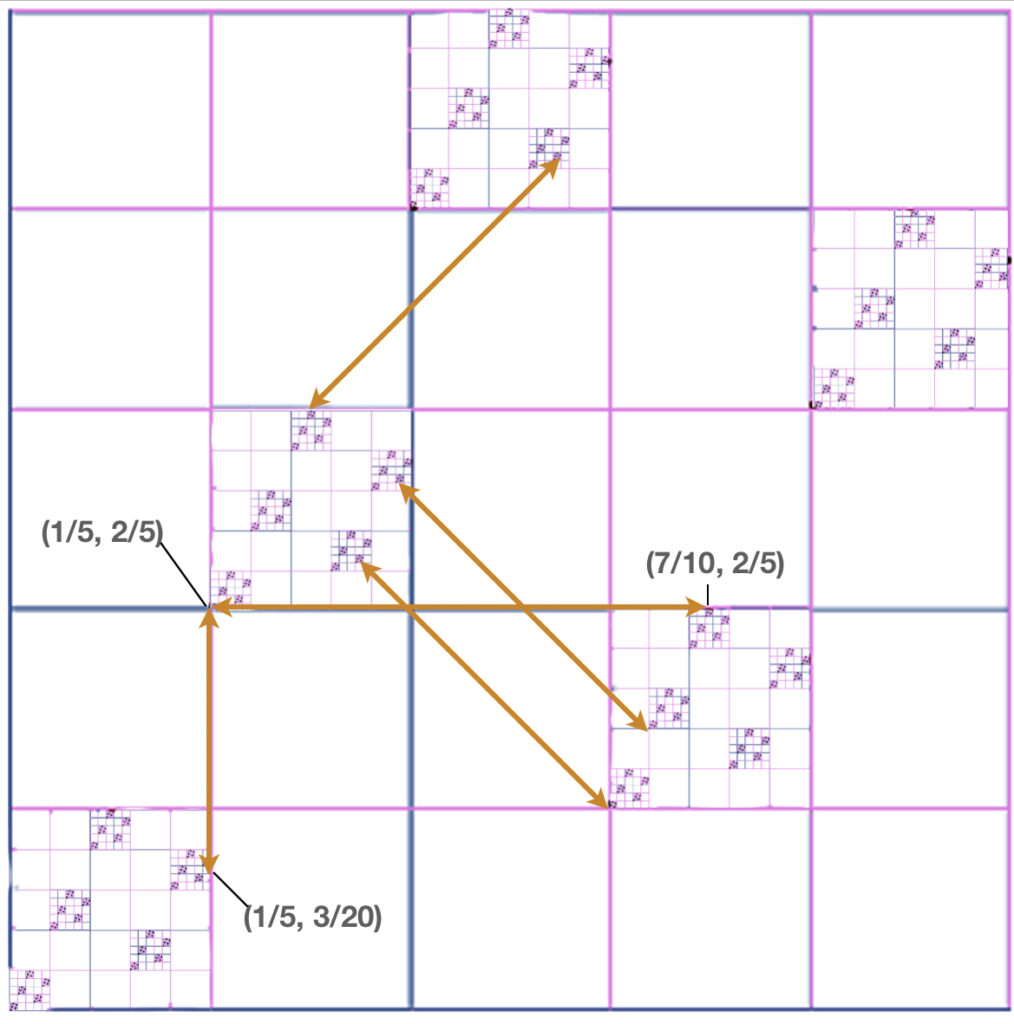
…with the result that we have two distinct queens in the position $Q$ sharing the same $x$  value:

$$ (x,y)_5 = (0.1, 0.2)_5 = (\frac{1}{5},\frac{2}{5})$$

and

$$ (x,y)_5 = (0.0444…, 0.0333…)_5 = (\frac{1}{5},\frac{3}{20})$$

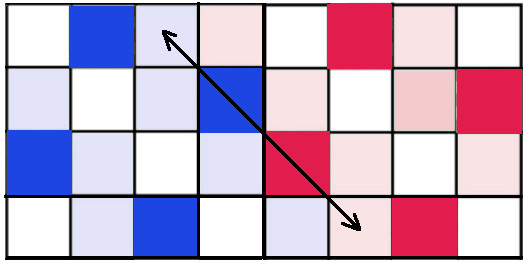
The two points can be seen here, along with (in red) many other queens in $Q$ which are mutally attacking, both by rook and by bishop moves:

And so we see that $Q$ is a total failure. Not only are there many members of this position that are hostile, but there are an uncountably many such failures!

As with the Rook and Bishop, the root difference between $B_{\omega}$ and $B_c$ has to do with topology. In the omega board, though infinite, it has a discrete topology with no limit points. In all of the cases with this continuum board, the queens which are attacking are limit points, belonging to members of the $Q_i$ sequence which bound the (rook or bishop) attack line from opposite sides of the line.

An Unsolved Problem

Although I have tried a number of variations on this “fractal” approach, I have not found any explicit (fractal or otherwise) constructions of a queen position on the continuum board $B_c$ which is maximal unguarded one. That is, a set of points $Q \subset B_c$ defined by a closed-form computable function, such that for every horizontal and vertical line $\lambda$ intersecting $B_c$, there is exactly one point in $\lambda \cap Q$, and for every diagonal line, there is no more than one point in the intersection.

A Solved Problem

As with many such questions about exotic properties of infinite point sets, it possible that no such closed form solution may even exist for the unguarded queens on the continuum board.

For example, a very similar problem to the unguarded queens is about the existence of “Two Point Sets”. That problem has been solved and can be stated like this:

TWO POINT SET THEOREM: There exists a set of points $T \subset \mathbb{R}^2$ such that every line in the plane contains exactly two distinct points of $T$.

This is a tantalizing statement, as it is about points and lines in the plane which satisfy a rule about which lines contains which points. And as with our unguarded queen problem, the quirky aspect of this (proven) theorem is that it only shows that a solution exists, but does not give any clue as to what it would look like.

In order to prove a theorem like this, however, requires some rather exotic techniques which depend on some deep hypotheses in set theory such as the Axiom of Choice and others. In particular, what is needed is a technique called Transfinite Induction.

This is a mathematical tool of which I had not been familiar during my younger days, and which most folks would have difficulty understanding at all, given that the word “transfinite” itself starts with Cantor’s discovery that there are sets which are so large that they are “uncountable” by the infinite set of numbers 1,2,3 etc.

The Theorem

Using the techniques mentioned above, it turns out that not only will we be able to prove the existence of an unguarded queen solution as defined above, but an even stronger result, which has no equivalent statement on either the finite boards or even the countably infinite omega board.

We first begin with a definition:

DEFINITION: a chess position $Q \subset B$, satisfies the Super Queen property on $B$ if every horizontal, vertical AND (45-degree) diagonal line $\lambda$ intersecting $B$ contains exactly one member of $Q$.

Note that this is property is called super, because the property is not satisfied by any queen positions on the finite or countably infinite chess boards. On those boards, a queen position can be rook-maximally guarded positions, but not Bishop-maximally guarded. There will always be diagonals without queens controlling them.

The theorem we will prove in the next (and final) post on the topic will be the following:

SUPER QUEEN THEOREM: On the open continuum board $B = B_{I}$, where $I = (0,1) = \{ x: 0 \lt x\lt 1\} $, there exists a queen position $Q$ having the Super Queen property.

In other words, there is a position $Q$ on the board such that for every horizontal, vertical and diagonal line that intersects the board $B_{I}$, there is exactly one Queen on that line that belongs to $Q$ !

Stay tuned.