Category: Geometry

Part VII Episode 2 of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

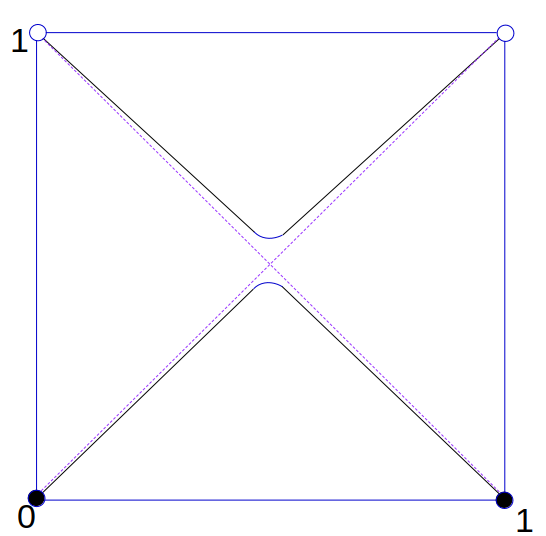
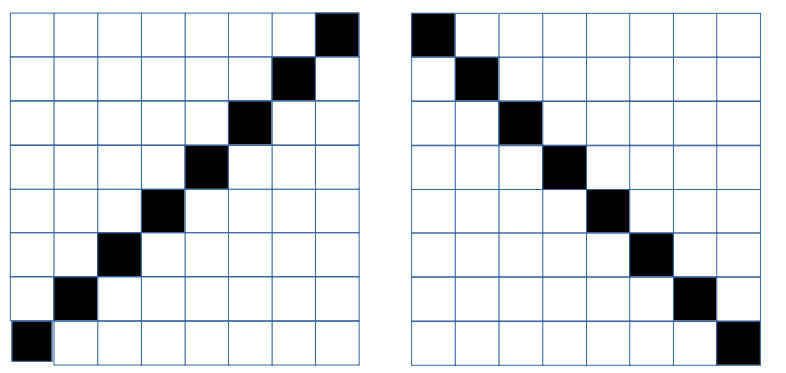
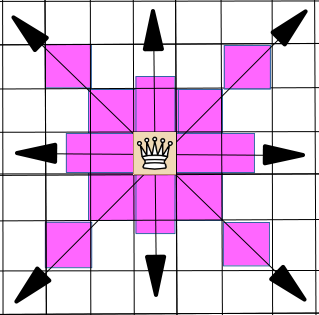
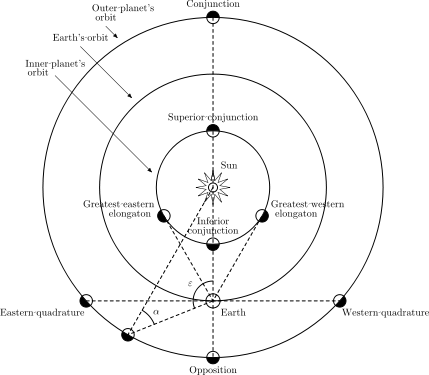
We are nearing the end, but still there is the tallest mountain to climb. We need to prove the SUPER QUEEN THEOREM, which says that not only is there a chess position $Q$ to the unguarded queen problem on the unit continuum board $B_c$ (where $c$ are is understood as all reals in the open unit interval (0,1)), but that in fact that solution satisfies the Super Queen property — which is to say, that not only is there exactly one queen on every rank and file (“Rook Maximal”), but that there is also exactly one queen on every diagonal (“Bishop maximal”). This is not possible on finite boards because we run out of places on diagonals to put the queens that don’t attack an existing queen by a rook move.

Note: we exclude the endpoints 0 and 1 from the intervals to remove the “degenerate” diagonals on the corners, and so ensure that all rows, columns and diagonals are of positive linear measure. If they were included, then only one of the two degenerate diagonals through (0,0) and (1,1) respectively could be admitted and the “super queen” property would not hold.

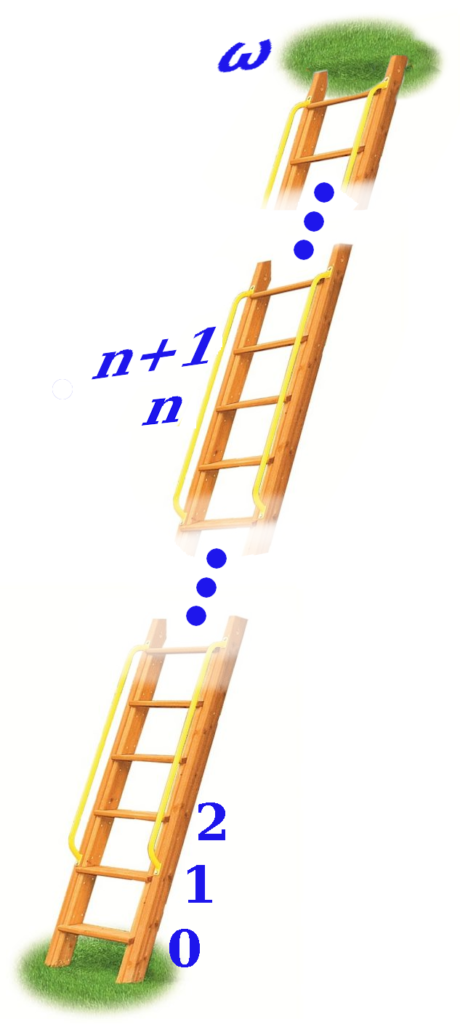
Climbing an Infinite Ladder

To prove this theorem, as mentioned in the previous post, we will need to use a technique called Transfinite Induction. This is a concept which extends a more conventional technique called Mathematical Induction. The general idea of regular induction in mathematics can be expressed using the metaphor of a ladder:

Mathematical Induction: If you can prove that

1. you can get on the first rung of a ladder, and
2. you can also prove for any N that
             if you can get to rung $N$,
             then you can also get to the next rung $N+1$,

then you have proven you can go all the way up the ladder.

This does not seem very deep, and in fact seems obvious, but it is a technique used in many parts of mathematics. For example, consider the theorem:

THEOREM: For every integer $n \ge 1$, the odd sum  $1 + 3 + 5 … (2n-1)$ is a square, and in fact

$$S_n = 1 + 3 + 5 … (2n-1) = n^2\tag{**}$$

For example, for $n=1$, $1 =  1^2$, for $n=2$, $1 + 3 = 4 = 2^2$, and so on.

PROOF: We shall use (regular) mathematical induction. The first step is to prove we can get on the “first rung”, so we look at $n=1$ and can see that indeed $1 = 1^2 = (2n-1)^2$. For the next step, suppose that formula (**) holds for a specific $n = N$, that is, for a specific $N$ we have:

$$S_N = 1 + 3 + 5 … (2N-1) = N^2\tag{***}$$

We need to show that (**) also holds for $n= N+1$. We can write

$$S_{N+1} = 1 + 3 + 5 …  (2(N+1)-1)^2$$

$$ = 1 + 3 + 5 … + (2N -1)^2 + (2(N+1)-1)^2$$

which by definition can be rewritten:

$$ = S_N + (2(N+1)-1)^2$$

and by the assumption (***) we have

$$ = N^2 + (2(N+1)-1)^2$$

which simplifies to

$$ = N^2 + 2N + 1 = (N+1)^2$$

which is formula (**) with $N+1$ substituted for $n$. We have just proved the second part of induction, which is that if (**) is true for $N$ then it is also true for $N+1$, and so the theorem is proved. QED.

The Rational Super Queen

As a first step toward proving the Super Queen Theorem on the transfinite board $B_c$, we will first prove the analogous theorem on the rational unit board $B_{\mathbb{Q}}$, where $\mathbb{Q}$ is understood as the set of all rational numbers between 0 and 1 exclusive.

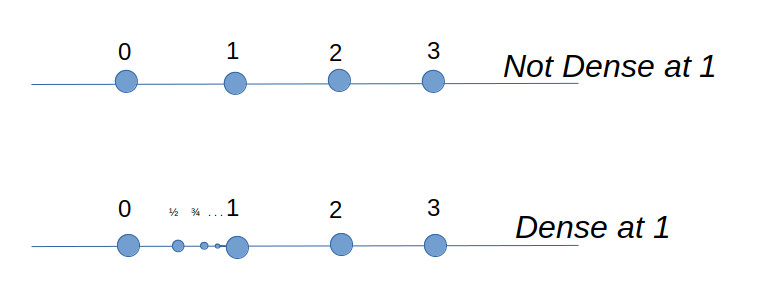
Referring back to the previous article on the Rook, both the rational unit board and the omega board have a countable infinity of “squares”. And as in that case, what makes the situations different is that the omega board (whose coordinates are integers) has a discrete topology, while the rational numbers are dense, and no square has a unique square “next to” it.

It should be noted that when restricted to just rational points, the concept of rook and bishop lines restricted to $B_{\mathbb{Q}}$ makes sense. The reason is that for any two “rational” points $p,q \in B_{\mathbb{Q}}$,, and any two rook or bishop attack lines $\lambda_p,\lambda_q$ which pass through $p$ and $q$ respectively, that their intersection is either empty or another rational point $r \in B_{\mathbb{Q}}$. That is, you will never have two points on the board whose common points of attack are irrational points outside of $B_{\mathbb{Q}}$. (Proof left to the reader)

Let us define $\Lambda$ to be the set of all rook and bishops lines (ie, all Queen lines) in $B_{\mathbb{Q}}$. Then we have

The Rational Super Queen Theorem: There exists a queen position $Q$ on the rational unit board $B_{\mathbb{Q}}$, such that for every queen line $\lambda \in \Lambda$ the intersection $\lambda \cap Q$ has exactly one point $q \in B_{\mathbb{Q}}$. That is, every Queen attack line in $B_{\mathbb{Q}}$ is occupied by exactly one queen in the position $Q$.

We will prove this theorem by (regular) mathematical induction. To do this we will need some definitions and to prove some  lemmas first.

Definition: a set $S$ is Well Ordered if there is an operator (which we will call $\le$), such that for all $x,y,z \in S$ we have

1.  $x \le x$
2.  Either $x \le y$ or $y \le x$
3.  if $x \le y$ and $y \le z$ then $x \le z$
4.  if $x \le y$ and $y \le x$ then $x = y$
5.  (Well Ordering): For any subset $T \subset S$, there exists a “smallest” element $x \in T$, ie, so that $x \le y$ for all $y \in T$.

The first four conditions describe “total ordering”, while the fifth (important) condition is what makes a “well ordering”. The principle of Mathematical induction is equivalent to the statement that the natural numbers $\mathbb{N}$ is well ordered.

Example 1: The positive integers $\mathbb{N}$ are well-ordered with the usual numeric ordering $\le$.

Example 2: The set of all integers $\mathbb{Z}$ is NOT well-ordered under $\le$, because $\mathbb{Z}$ itself is a set having no smallest value (violating condition 5).

 

Theorem 1:  The rational points $(x,y) \in B_{\mathbb{Q}}$ have a well ordering (but not the usual one $\le$).

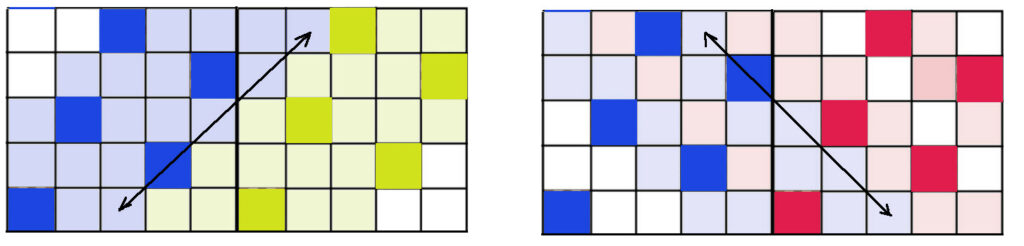
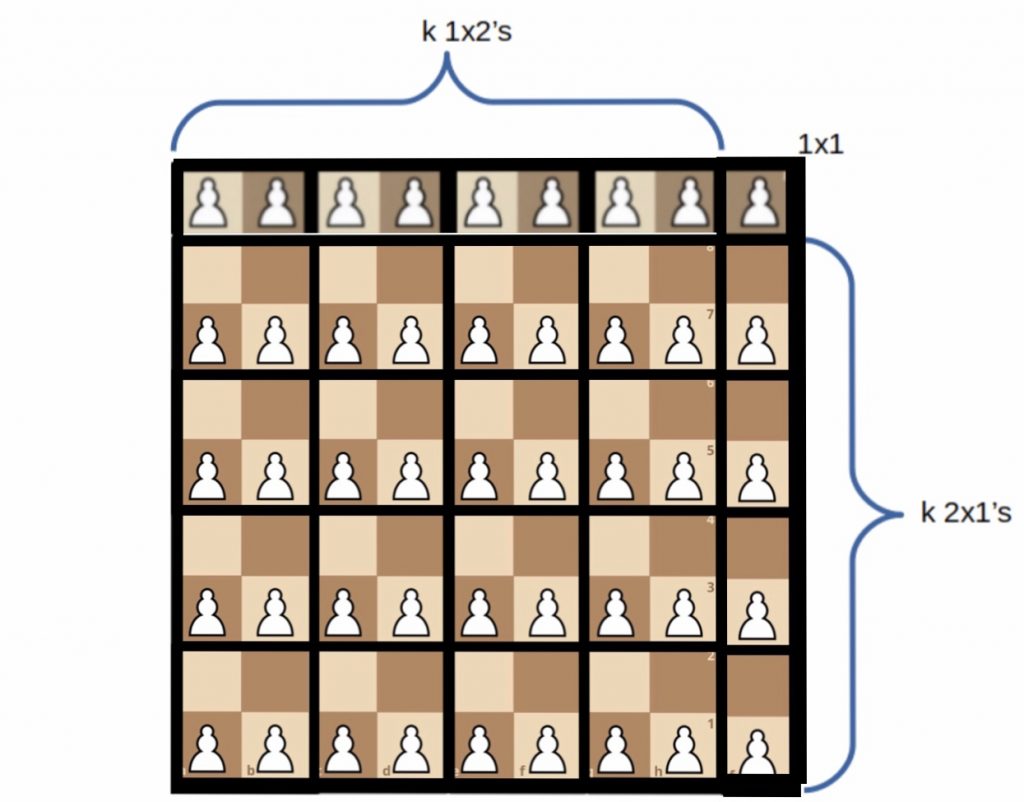
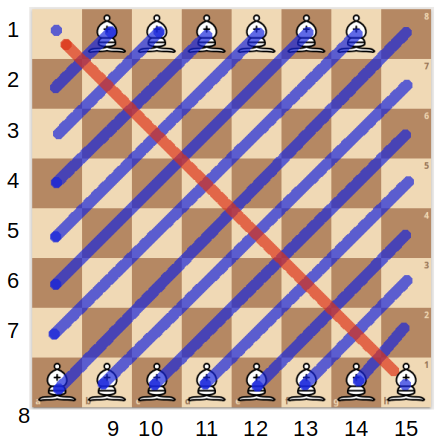
Proof: It is known that the positive rational numbers $\mathbb{Q}$ are countable; that is, that there exists a function mapping the natural numbers $\{1,2,3,…\}$ to $\mathbb{Q}$ in a 1-to-1 way. To see that, observe that they can all be represented as fractions $p/q$ in a square array whose x and y coordinates indicate the numerator and denominator (below). Note that fractions that are not in simplest terms (e.g. 2/2) are skipped.

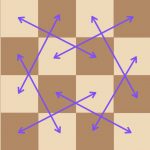
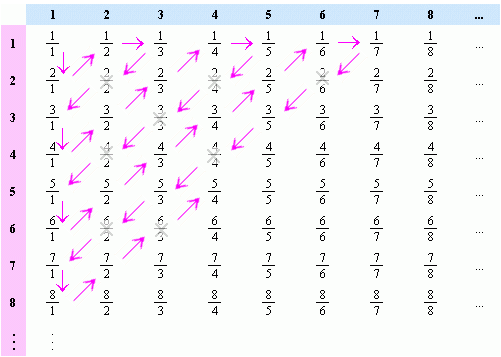As the arrows suggest, we can then “thread” the numbers onto a line, and number them by the order they appear, like this:

$$x_n = \frac{1}{1},  \frac{2}{1},  \frac{1}{2},  \frac{1}{3}, \frac{3}{1}, . . . $$

$$n = 1,  2,  3, 4, 5, . . . $$

This gives us a function $Q(n)$ which takes the integer $n$ to $x_n$. And so, we can define our new “ordering” (call it $\prec$) on the positive rationals by defining $x_n \prec x_m$ if and only if $n \le m$ in the usual sense. And this ordering is well-ordered, because for any subset $S$ of positive rationals, one simply considers the inverse set $S’ = Q^{-1}(S)$. SInce $S’$ is a subset of the positive integers, there must be a smallest one $m \in S’$, and by definition this is also the “smallest” in $S$, ordered by $\prec$.  QED

Theorem 3:  The rational points $(x,y) \in B_{\mathbb{Q}}$ have a well ordering.

Proof: We can follow a proof that parallels the one just given for Theorem 2. For we can use the inverse function $Q^{-1}(x)$ to map all rational points $(x,y)$ to non-negative integer points $(m,n)$, and by arranging them in a similar grid as above, “thread” the integer grid with a single integer line, and then use the inverse of this mapping to map the well-ordered integers to the rational points.  QED

Theorem 4:  The set $\Lambda$ of queen lines on the rational board is countable and can be well ordered.

Proof: Each (non-degenerate) queen line can be identified by a pair of distinct rational points $(x,y)$ and $(z,w)$ on the board which belong to it. The rational points are well ordered and (by the same arguments above), the pairs of such points also have a well-ordering.

Proof of The Rational Super Queen Theorem

Our goal is to prove that we can construct a position $Q = \{ q_0, q_1, . . . \}$ on the unit rational board, such that every queen line $\lambda \in \Lambda$ contains exactly one and only one element $q \in Q$.

By Theorem 4, the queen lines $\Lambda$ are countable. This means that we can assign an index $n$ to each of them which might as well be the integers 0,1,2…), which also gives them a well-ordering.

In addition, the points on the rational board itself is countable and has a well-ordering.

To prove the existence of a position $Q$ we shall use (regular) mathematical induction.

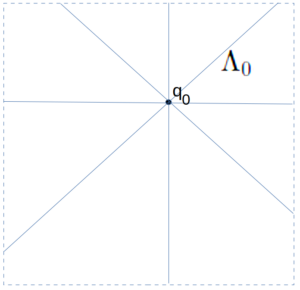
For step zero, we simply define $q_0 = b_0$ where $b_0$ is the first element in the well-ordering of the board. We also define $\Lambda_0$ to be the set of (four) queen lines which pass through $q_0$. Let us also define the set $Q_0 = \{ q_0 \}$.

For step 1, we consider the set of all queen lines which are not in $\Lambda_0$, and take the queen line $\lambda = \lambda_\alpha$ whose index $\alpha$ is the smallest among those. We then exclude from this $\lambda$ (considered as a set of points in the board) all points where it 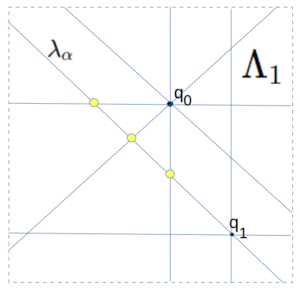intersects $\Lambda_0$ (shown here in yellow). This intersection is a finite set of points, and so we can pick for $q_1$ any other point on $\lambda$ not in this intersection. We then can define $\Lambda_1$ to be the set of all queen lines which pass through the set $Q_1 = \{ q_0, q_1 \}$. Note that $\Lambda_1 \supset \Lambda_0$ and is itself finite. We also note that any place where $\Lambda_0$ and $\Lambda_1$  share a point, those points are not in $Q_1$.

To generalize this last step inductively, for step $n+1$, we consider the set $S \subset \Lambda $ of all queen lines which are not in ${\Lambda_n}$, and among them choose a queen line $\lambda = \lambda_\alpha$ whose index $\alpha$ is the smallest within $S$. We can do this because ${\Lambda_n}$ is a finite set of queen lines, and so the remaining set is non-empty (in fact, countably infinite), and $\Lambda$ is well-ordered. We now consider the set of all intersections of $\lambda$ with lines in ${\Lambda_n}$. As before, this is a finite number of intersections and so we can choose for $q_{n+1}$ any point in the (infinite) queen line $\lambda$ not in this set, and define $\Lambda_{n+1}$ to be all queen lines passing through points $Q_{n+1} = Q_{n} \cup \{q_{n+1}\}$.

We now assert that (1) this tower of inclusive sets

$$\Lambda_0 \subset \Lambda_1 \subset \Lambda_2 . . . $$

is exhaustive, and its union will eventually include every single queen line $\lambda \in \Lambda$. In other words, the union is itself $\Lambda$. And furthermore, (2) the union of the tower of sets

$$Q_0 \subset Q_1 \subset Q_2 . . . $$

is our desired position $Q$ and that every member of $\Lambda$ meets $Q$ in exactly one point. The proof of this is below:

(1) To see that the $\Lambda_n$ tower is exhaustive, assume that this was not the case, and that there was some $\lambda$ that was missing from the tower, and so let us choose $\lambda_\beta$ to be the smallest of these missing ones in the well-ordering of $\Lambda$. But now consider how we constructed the set $\Lambda_{\beta + 1}$.  By construction, it was the union of $\Lambda_{\beta}$ with the  $\lambda_n$ with the smallest index $n$ which was not in $\Lambda_{\beta}$. But this means that $n$ must be greater than $\beta$, and so $\lambda_\beta$ should have been chosen at that step because it has a smaller index and is not in $\Lambda_{\beta}$.

(2) To see that every member $\lambda$ of $\Lambda$ meets $Q$ in at least one point, simply note that $\lambda$ must belong to $\Lambda_n$ for some smallest $n$ (since the union was exhaustive). But $\Lambda_n$ was defined to be all queen lines passing through $Q_n$, and so $\lambda$ must meet at least one element of $Q_n \subset Q$. But the points already chosen were selected from a set that excluded pairwise intersections of members of $Q_n$, and so $\lambda$ cannot possible meet any more than one element (as pairwise intersections were excluded). Hence $\lambda$ meets $Q_n$ at exactly one point, and by the construction, no later $Q_m$ sets meet $\lambda$ at all.

QED

This proof is remarkable, because nothing like it is possible with the finite boards. The thing which makes this work, is that at each step we are only removing a finite number of points from an infinite board, and so we can always find more in the remaining infinite sets to satisfy our conditions. Unlike the finite case, it did not matter whether any “queen line” was a rook or bishop style line. They were each treated equally in the set $\Lambda$ and the process of eliminating candidate points for the next step never exhausted the pool.

Having now proved the “Super Queen” solutions exists for the rational board, we are ready to pull out the big guns in the next post and deal with the Super Queen solution on the transfinite real board.

 

 

Part V of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

Review

We — that is, I — have been studying the (classic) “unguarded” chess puzzle, which is to say, how to pack as many of one chess piece on a chess board without any of the pieces attacking any others. But with the twist, that the board may be infinite, and possibly uncountably infinite. In the last post we saw that the set of maximal unguarded solutions for the Rook on the board $B_A$ (for any set $A$) had an interesting mathematical property, that they could be represented as the permutation group on the set $A$. In later posts we will see that the Queens also have some interesting properties, some of which can already be seen in our current focus on the Rook.

What is Topology and Why does it Matter?

The glib definition of topology is “rubber sheet geometry”, which is to say, the study of what properties are preserved in an object even if they are made of rubber and can be twisted and stretched but not “torn”. For example, a solid ball and a solid cube can be deformed into each other just by stretching, but to deform a ball into a 1-holed doughnut you would need to puncture the ball to make the hole — which is not allowed.

One way in which a “topology” can be defined on a space is by specifying the way in which two points are “close” to each other, or whether two points can be “connected” by a continuous path.

We have been defining “chess boards” as two-dimensional things (denoted $B_A$) whose “squares” are identified with coordinates (x,y), where the x and y are in some subset $A$ of the real line $\mathbb{R}$. For example, the standard 8×8 chessboard we called $B_8$ uses the coordinates in the subset $\mathbb{Z}_8 = \{ 0, 1, 2, … 7 \}$ (though we could just as easily have taken {1, … 8} ). Among the other coordinate sets $A$ we could consider are the whole numbers, the rationals, the algebraic numbers, and the non-negative real numbers, or for that matter the whole real line.

Topological Density

To see why questions about chess puzzles on various boards $B_A$ may have different answers depending on topology, consider that one of the properties of a subset of $\mathbb{R}$ is called density. A set $A \subseteq \mathbb{R}$ is said to be dense at a point $x \in A$ if for any other point $y \in A$ where $y \neq x$, there exists another point $z \in A$ strictly between them, ie, such that $(z-x)*(z-y) < 0$. The set A is everywhere dense if it is dense at every point of A, and nowhere dense (also called “discrete”) if it is not dense at any point of A.

For example, the whole numbers $\mathbb{W}$ is nowhere dense because there are no other integers between n and n+1. Meanwhile, the rationals $\mathbb{Q}$ are dense, because if $p$ and $q$ are two distinct rational numbers (ie, can be expressed as an integer fraction $m/n$), then it can be shown that $(p+q)/2$ is another rational strictly between them.

And so, to see the reason why density is relevant for chess, simply note that the moves and attack regions for both the King, Pawn and Knight are defined by the squares *adjacent* to their current location, and on a board $B_A$ where $A$ is everywhere dense, there is no such thing as an adjacent square, because there is always another square in A in-between. In other words, the “unguarded” puzzle for Kings, Pawns and Knights does not make sense for dense sets $A$ such as rationals, algebraics, or reals. Meanwhile, because the attacks of Bishops, Rooks, and Queens is defined in terms of directions on the board (horizontal, vertical, diagonal), they have well-defined meanings even on everywhere dense boards.

Connectedness

Strictly speaking, a set is topologically connected if it cannot be represented by a union of two disjoint open sets. By that definition, a set like the integers or the rationals is nowhere connected. For example, the rationals can be represented as $\mathbb{Q} = \mathbb{Q}^+ \cup \mathbb{Q}^-$, where $\mathbb{Q}^+$ and $\mathbb{Q}^-$ are the sets of rationals greater and less than $\sqrt{2}$, respectively. These are both open sets because for any rational number $x \in \mathbb{Q}^+$, all other rationals (sufficiently close) to $x$ are also in the same set.

Nevertheless, we can still define “weaker” forms of connectedness on the rationals, in the sense that the closure of $\mathbb{Q} \subset \mathbb{R}$ is connected. There are also other more general definitions. A set is considered connected, intuitively, if you can get from any place in the set to any other by a “connected” path lying wholly within the set (whose definition needs to be made clear).

For example, suppose we take the set of whole numbers $\mathbb{W}$, and define that two elements $m, n \in \mathbb{W}$ to be “weakly connected” if they differ by no more than 1. So, 2 is connected to 3 and 1, as well as itself, but 2 is not connected to 4. More generally, we can say that two subsets A and B of $\mathbb{W}$ are weakly connected to each other, if there exists a member a in A and b in B such that a and b are connected. Finally, we can define a single subset $A \subseteq \mathbb{W}$ to be weakly connected, if for any two elements $a,b \in A$, there exists a finite sequence of elements $\{ a_i \} \subset A$ such that $a = a_0, a_n = b$, and where $a_i$ and $a_{i+1}$ are connected for all $i = 0…n-1$.

With this definition, we can see that the set $A = \{0,1,2,3,4\}$ is a weakly connected set, but that $A=\{0,1,3,4\}$ is not connected, because there is no way to to get from 1 to 3 by connected elements in $A$ (2 is missing and forms a gap).

The reason all this matters is that we will see that for the solutions to the unguarded rook problem, the topology of those solutions differs when we go from the infinite integer board $B_{\omega}$ to the infinite rational board $B_{\mathbb{Q^{+}}}$ or real board.

The Topology of the Integer Board

Just as with the rationals, we can define “weakly connected” on the integer board $B_{\mathbb{W}}$, by first specifying that two squares a and b are “weakly connected” if they are a Kings move away from each other, that is, one square away horizontally, vertically, or diagonally. And by extension, we can say that any subset $A$ of $B_{\mathbb{W}}$, is connected, if any two members $a$ and $b$ of $A$ can reach each other, by a king moving strictly within the set $A$. From this point on, we will use “connected” to mean “weakly connected”, unless we say otherwise.

Connected Rook Theorem 1: On any finite board $B_n$, the only connected maximal solutions to the unguarded rook problem are the two diagonal solutions, ie the graphs of the function $y=\phi(x)$, where

$$\phi(x) = x$$

or

$$\phi(x) = n – 1 -x$$

PROOF

We first claim that if two squares in an unguarded rook solution are both connected to a third one, then all three must lie on the same diagonal (northwest or northeast). For, consider the case where square $a$ is connected to square $b$ along the north-east diagonal. We can go through and eliminate with an x all of the squares which are attacked by either $a$ or $b$. And what we see is that the only remaining square which a third rook can be placed and still be attached to $a$ is the lower-left corner.

By repeated application of this claim, what we have just shown is that all of the rooks in a connected component of an unguarded rook solution must lie on the same diagonal. Since this is a maximal unguarded solution, there must be a rook on the first row somewhere. We now claim that it must either be on the leftmost square (forming the northeastern diagonal solution), or else the rightmost square (forming the northwestern diagonal solution). For suppose that the rook is anywhere else along the bottom row, and that (without loss of generality) that it is part of a northeasterly diagonal.

Once again, by a process of eliminating all other squares under attack by the northeasterly diagonal line of rooks, we can see that this leaves a disconnected square in the upper left corner as the only available locations of the rooks that must occupy the remaining rows and columns. But none of these squares are connected to the northeast diagonal, and so a maximal unguarded solution cannot be constructed in this manner that is also connected.

QED

Connected Rook Theorem 2: On the infinite integer board $B_{\omega}$, the only connected maximal solution to the unguarded rook problem is the main diagonal solution, $\phi(x) = x$.

Proof: Clearly the above solution is maximal. Suppose that there is another maximal solution where there is a rook located at a position $P = (m,n)$, where (without loss of generality) we can assume $m > n > 0$. By eliminating all cells attacked by this rook, we now have a board segmented into four non-empty regions, (I, II, III, IV),  each of which would be disconnected from each of the others, save for their connection to the rook at $P$.

By the same argument previously, either $P$ connects regions I to IV by the north-west diagonals, or else it connects regions II and III, by the northeast diagonals. If we choose to join regions II and III, then region III (including P) is an $m x n$ rectangle, in which we would have to fit $m$ rooks, even though we only have $n$ rows. This would force at least two rooks to occupy the same rows, which is not allowed. This leaves us with P joining up regions I and IV, by a northwest diagonal.  Now region I only has $m-1$ columns, while region IV has only $n-1$ rows, and so we have only a finite number of additional rooks we can add to this solution (region II not being connected to P). Thus neither option allows us to define a maximal solution to the unguarded rook problem, meaning that we must conclude that only the case where $m=n$ is valid.

QED.

Unguarded Rooks on a Rational Board

While we could take the entire set $\mathbb{Q}$ of rational numbers, for our purposes it suffices to look at a much smaller but equivalent space, which is the unit interval of rational numbers, ie

$$ \mathbb{Q}^* = \mathbb{Q} \cap [0,1] $$

The set of rationals is countably infinite, and so our board $B_{\mathbb{Q}^*}$ has the same number of “squares” as the infinite integer board. Nevertheless, the unguarded rook problem on this board has a surprising answer in store for us, given by the following theorem:

Connected Rook Theorem 3: There are an infinite number of connected maximal unguarded Rook solutions on the rational unit board $B_{\mathbb{Q}^*}$.

Comment: Just so you can see how on earth this could be possible, consider just one valid solution, defined on $\mathbb{Q}^*$ by the function:

$$\phi(x)=
\begin{cases}
\frac{x}{2}, & \text{if $x \in [0, \frac{2}{3})$} \\
2x – 1, & \text{$x \in [\frac{2}{3}, 1]$}
\end{cases}
$$

The function $\phi(x)$ is a piecewise-linear function, which is a bijection on the set $\mathbb{Q}^*$.

The graph on $B_{\mathbb{Q}^*}$ shows that the placement of the rooks on the board looks like this:

what makes this work is that linear functions are invertible on the rational numbers, and that the rational numbers (unlike the integers) are *dense*. The same trick would not work on the integers, because you can’t apply y = x/2 to the odd integers and get another integer back.

Just to remind the reader of what this picture is about, that thin line is a chess position, consisting of a set of infinitely many rooks along that line, so an (infinite) magnification would reveal them, like this:

This example is just one of many other such piecewise-linear functions which do the trick. The only requirement is that the functions must be strictly monotonic (increasing or descreasing) on the interval $\mathbb{Q}^*$, and (to ensure it is maximal), covers the entire interval, either by $\phi(0) = 0, \phi(1) = 1$ or else $\phi(0) = 1, \phi(1) = 0$.

It turns out that the number of such functions is infinite. This can be seen easily by just noting that there was nothing special about the bend at $x=2/3$, and you could create a similar function with a bend on any other rational number between zero and one, of which there are countably infinite many of them.

Fractal Content

The (two-dimensional) density of the Rook solutions is zero, since lines have zero area. This is the case for all three pieces Rook, Bishop and Queen. But we can still compare the relative density of each of these pieces, by measuring the (one-dimensional) “fractal” content of the positions. For example, the fractal content of the solution shown above is simply the length of the two line segments, which is $2\sqrt{5}/3 \approx 0.75$. But we can actually do much better, by pushing the “corner” of the two lines toward the bottom right like this:

in which case the fractal density is $\sqrt{82}/10 \approx 1.82$. As can be seen, by pushing further the rook solutions can attain fractal densities as close to 2 as we like.

Uncountably Many Solutions

We showed above that there are an infinite number of connected maximal Rook solutions on the rational interval board $B_{\mathbb{Q}^*}$. But you can actually say a lot more; in fact the number of such solutions can be shown to be uncountably infinite, which is to say, there are at least as many of these solutions as there are real numbers (the infinity of the continuum) !

One way you can prove that the number of solutions is uncountable, is to construct a mapping between the (uncountable) set of all infinite decimals between 0 and 1, and a piecewise-linear function with rational coefficients, whose graph is a maximal connected solution of the unguarded Rook problem.

To do this, we first define for each digit from $i = 0 . . . 9$, a different piecewise linear function $f_i()$ on the unit square, simply by mapping the digits to different “bend locations” in the square (having rational coordinates):

Next, we take the unit square and along the main diagonal, lay out an infinite number of smaller squares, each half the size of the previous:

We now show how to map each infinite decimal fraction $z$ (e.g. $z = 0.2739 . . .$ ) to a specific piecewise-linear function $F = F_z(x)$ on the unit square. For each of the smaller squares we have placed inside the unit square, we go through the decimal digits in $z$ and for each digit $d$ define the corresponding function $F_z(x)$ restricted to that range by $F_z(x) = f_d(x)$, corresponding to that digit $d$.

As these infinite number of squares converge to the point $(1,1)$, we define $F_z(1) = 1$, which gives a complete definition on the whole unit interval. Since this mapping is injective, this means that the number of piecewise linear functions with rational coefficients is at least as large as the number of reals on the unit interval, which is uncountably infinite. This completes the proof.

So yes, there are a lot of them. And again, the reason this is so different from the integers has to do with the topological density of the sets.

Just to close the loop, if we look at the full real interval $I  = [0,1] \subset \mathbb{R}$, it is actually much easier to construct topologically connected (in fact, compact) maximal unguarded Rook solutions. To construct such solutions, all that we require is that it be the graph of a function $y = \phi(x)$, where $\phi$ is a bijection on $[0,1]$ such that it is continuous and monotonically increasing or decreasing. That is, if $x > y$ then $\phi(x) > \phi(y)$. A simple set of examples of this are the powers of x, such as $\phi(x) = x^2, \phi(x) = x^3$, and so on.

As with the rational board case, with higher powers of x the curve begins to hug the bottom and right side of the board, with a curve length approaching 2. But can we do any better, or is 2 the largest 1 dimensional fractal content we can attain for connected unguarded rook solutions? The answer is given by the following theorem:

Fractal Content Rook Theorem: The path length of  a connected maximal unguarded Rook solution on the unit interval is not more than 2. That is, the length of any curve $y = \phi(x)$ on the unit interval $[0,1]$ where $\phi(x)$ is a continuous monotonically increasing function from 0 to 1 on the interval is less than or equal to 2.

Proof: We will need to use a little bit of calculus to do this. First, we parameterize the curve by $c(t) = (x(t),y(t))$ where the parameter $t$ ranges from 0 to 1, and

$$
\begin{cases}
x = x(t) = t \\
y = y(t) = \phi(x(t))
\end{cases}
$$

From this we can compute the path length $s$ given by the integral (ie, sum):

$$s = \int_{t=0}^1 \frac{ds}{dt} dt$$

where $ds$ is the incremental increases in the path distance by $(dx,dy)$, given by

$$ds = \sqrt{dx^2  + dy^2}$$

For those unversed in calculus, think of $ds$ as just very small line segments into which the curve has been broken, and use Pythagorean Theorem). Now $dx/dt = 1$ since $x=t$, and $dy/dt \ge 0$, given that $y = \phi(x)$ is monotonically increasing. We can thus take advantage of the inequality

$$ \sqrt{a^2 + b^2} \le \sqrt{a^2 +2ab + b^2} = (a + b) $$

when $a,b \ge 0$ to assert that (formally)

$$\frac{ds}{dt} = \sqrt{(\frac{dx}{dt})^2  + (\frac{dy}{dt})^2} \le \sqrt{(\frac{dx}{dt} + \frac{dy}{dt})^2} = \frac{dx}{dt} + \frac{dy}{dt}$$

and so we can conclude (since x(1) = 1 and y(1) = 1):

$$s \le \int_{t=0}^1  \frac{dx}{dt} + \int_{t=0}^1\frac{dy}{dt}dt = 1 + 1 = 2 $$

which was to be proved. QED

We have now pretty much exhausted the study of unguarded Rooks, so it’s time to touch base briefly on the Bishop, before we move on (at last) to the unguarded Queens.

Part III of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

This is part III of my series of posts on the “Chess Density Problem”. In Part I, I introduced the problem and laid out some definitions to clarify what I meant by some of the terms such as “Board” and “Density”. In Part II I gave everyone a breather.  Hope you’ve rested up. In this one the math is going to be a bit thick, but the purpose of it all will be to prove this first theorem:

The Chess Density Theorem – Pawn, Knight and King

DENSITY THEOREM 1: For Pawns, Knights, and Kings, their asymptotic density $\delta$ on the infinite board ($B_{\omega}$) is given by:

1.1) $\delta(P) = 1/2$.

1.2) $\delta(N) = 1/2$.

1.3) $\delta(K)= 1/4$.

In other words, on an infinite chess board, you can pack at most half of the squares with “friendly” Pawns or friendly Knights, and only a quarter of the board with friendly Kings. As a reminder, by “friendly” I mean that none of the pieces are threatening each other by standard chess rules.

Plan of Attack

As a starting point, we can note that the solutions found on the standard 8-board can be seen as built up from simple “tile” patterns made of identical small boards:

 

These tiles each have the densities that are claimed by the Density Theorem above. If we can prove that no such tiles can have a greater density, we can show that this must hold for larger boards. The way which we will do this is to define a precise way to “measure” the density of any arbitrary block of squares, and prove some useful properties of that measure-function.

Definitions

It always helps to define things precisely. There are a lot of fancy symbols, but the general ideas should be clear.

The Pieces

The six standard Chess pieces are King, Queen, Bishop, Knight, Rook, and Pawn, which we will denote with the initials {K,Q,B,N,R,P}, respectively. To this set we will also add the “Empty” piece, denoted $\varnothing$, which indicates that a square is empty.

The set of all pieces including the empty piece will be denoted

$$\mathscr{P} = \{K,Q,B,N,R,P,\varnothing \}$$

We include that “empty” piece to allow us to explicitly specify that a square is empty.

Control Zones

DEFINITION: The control zone of a piece X at position $x$ on a board B is the set of all other locations $y \in B$ which (by the standard rules of chess) are subject to attack by X (with no other pieces on board).

The Control Zones of the Pawn, Knight and King are shown in blue below:

 

 

 

 

 

 

One thing to note about these three pieces is that their control zones can be defined by a specific finite set of integer offsets from the location of the piece itself. The same cannot be said for the other three pieces (Rook, Bishop, Queen), as their Control Zones are not defined by a fixed set of offsets, but a set of directions on the board, by which they can attack (again, assuming that there are no other pieces blocking the way).

The Control Zone directions for the Rook, Bishop and Queen are shown below.

 

 

 

 

 

 

As we begin to work with the infinite boards we will see that this difference between the two sets of pieces profoundly affects how “dense” they can be.

In particular, on infinite boards the control zones of the Rook, Bishop and Queen are also infinite.

Chess Positions

A lot of the definitions below are just stuff I made up. If they correspond to standard chess terms I will mark them with (standard). If I feel that the definition may not be clear, I will give an example as well.

DEFINITION: For a given board $B$ and any subset $\Omega \subseteq B$, a chess position $\Phi$ on $\Omega$ is simply a function $\Phi$ that for each location $x \in \Omega$ there is a piece $p \in \mathscr{P}$ given by $p = \Phi(x)$ at that location. That is, it is a function

$$\Phi: \Omega \rightarrow \mathscr{P}$$

For all of the chess positions we are considering for this puzzle, we only have one kind of piece on the board at the time. And so we will call them “Pawn-positions”, “Queen-positions” etc. Thus if $\Phi$ is a King-position on $\Omega$, then it is a function $\Phi: \Omega \rightarrow \{K, \varnothing\}$.

DEFINITION (standard): A Position is called Unguarded if no piece in the position is in the control zone of another piece. In other words, unguarded positions are positions where the pieces are all “mutually friendly”.

DEFINITION: If $n > 0$ is an integer and $X$ is a (non-empty) chess piece, define $\mathscr{U}(n,X)$ to be the set of all “Maximally Unguarded” X-positions using only piece $X$, on the n-Board. That is, if there are no other unguarded positions with a larger number of pieces.

Measurement of Positions

DEFINITION: For any position $\Phi$ on $\Omega$, we can define the size ($\vert \Phi \vert$) and weight ($\Vert \Phi \Vert$) of that position by the number of elements in its domain $\Omega$ and the number of non-empty locations in its range, ie

$$\vert \Phi \vert = \vert \Omega \vert$$

$$\Vert \Phi \Vert = \vert \{ x \in \Omega: \Phi(x) \neq \varnothing \} \vert$$

EXAMPLE: In the little 4-board below, there are four queens, and the rest are empty.

So, following the defintion above, the board $\Omega$ is the 4×4 board, and its position function $\Phi$ maps every square to the empty piece $\varnothing$ except for the four squares that are mapped to the Queen. The size of the position $\Phi$ is simply the number of squares in $\Omega$, ie $\vert \Phi \vert = \vert \Omega \vert = 16$, while the weight of the position is the number of squares mapped by $\Phi$ to the Queen, ie $\Vert \Phi \Vert$ = 4.

DEFINITION: The for any position $\Phi$ on some board $\Omega$ its Density (denoted $\delta(\Phi)$ ) is the ratio of its weight divided by the size of the position , ie

$$\delta(\Phi) =  \frac{\Vert \Phi \Vert}{ \vert \Phi \vert }$$

DEFINITION: The for any integer n>0, the n-Density (denoted $\delta_n(X)$ ) of a piece $X$ on the n-Board is the maximum density of all possible unguarded positions $\Phi \in \mathscr{U}(n,X)$ ie

$$\delta_n(X) =  \max_{\Phi \in \mathscr{U}(n,X) }\delta(\Phi)$$

EXAMPLE: So, in the previous example for the unguarded queens on the 4-board, it can be seen that:

$$\delta_4(Q) = 4/4^2 = 4/16 = 1/4$$

With all of these preliminaries out of the way, we can now define what we really mean by the density of a piece on an infinite board:

DEFINITION: The Asymptotic Density (denoted $\delta(X)$ ) of a piece $X$ on the infinite board $B_\omega$ is the limit (if it exists) of the n-Density $\delta_n(X)$ of piece X as $n \to \infty$ ie

$$\delta(X) =  \lim_{n \to \infty }\delta_n(X)$$

The Linear Density Measure

For each of the pieces mentioned in the theorem above, their claimed density is of the form $\delta = 1/m$, where $m$ is some positive integer. It turns out that working with density ratios directly is tricky, so we will look at a different “measure” of density that turns out to be easier to work with, as we break a large board into tiles.

So, suppose $w$ is the weight of an X-position $\Phi$ on a set $\Omega$ of size $s$. Then the density $\delta$ is given by

$$\delta = \frac{w}{s}$$

and so if indeed $\delta=1/m$ then

$$1 = m\delta = m\frac{w}{s}$$

and therefore $mw = s$, which is to say that whenever a position has density 1/m, then we can also write

$$mw – s = 0$$

Using this fact, for any sub-position $\Upsilon \subseteq \Phi$ let’s define the “m-linear density” measure function $\Lambda_m(\Upsilon)$ by

$$\Lambda_m(\Upsilon) = m \Vert\Upsilon\Vert  – |\Upsilon|$$

Intuitively, what this measure value tells you is how much over or under the expected density a position is from $1/m$. if the value is exactly zero then the density is exactly $1/m$.  We now present a lemma (ie, a small theorem we can prove now and use later):

LEMMA 1: If $\Phi$ and $\Upsilon$ are two positions defined on disjoint subsets $S$ and $T$ of a board $B_n$, and $m > 0$ is an integer then

$$\Lambda_m(\Phi \cup \Upsilon) = \Lambda_m(\Phi) + \Lambda_m(\Upsilon)$$

that is, the m-linear density of the union of two disjoint positions is the sum of the m-linear densities of each.

PROOF: Follows immediately from the fact that the size of the union of disjoint sets is the sum of the sizes, and regrouping of terms:

$$\Lambda_m(\Phi \cup \Upsilon) = m\Vert\Phi \cup \Upsilon\Vert – \vert\Phi \cup \Upsilon\vert$$

$$=m(\Vert\Phi\Vert + \Vert\Upsilon\Vert) – (\vert\Phi\vert + \vert\Upsilon\vert)$$

and so, regrouping like terms:

$$=(m\Vert\Phi\Vert – \vert\Phi\vert) + (m\Vert\Upsilon\Vert -\vert\Upsilon\vert)$$

$$= \Lambda_m(\Phi) + \Lambda_m(\Upsilon)$$

QED (Quod Erat Demonstrandum = which was to be proved).

$\blacksquare$

LEMMA 2: There exists a positive constant $C > 0$ such that the 2, 2, and 4 linear densities $\Lambda(\Omega)$ of maximal unguarded positions $\Phi$ of Pawns, Knights and Kings on the n-board are bounded by the following expressions:

$$ \forall \Phi \in \mathscr{U}(n,P): 0 \le \Lambda_2(\Phi) <  C * n \tag{2.1} $$

$$ \forall \Phi \in \mathscr{U}(n,N): 0 \le \Lambda_2(\Phi) <  C * n \tag{2.2} $$

$$ \forall \Phi \in \mathscr{U}(n,K): 0 \le \Lambda_4(\Phi) <  C * n \tag{2.3} $$

PROOF: We will start with the formula for the Pawn; the other proofs will be similar. We first note that for the $2 \times 2$ tile $T$ for the Pawn case, the linear density is exactly $\Lambda_2(T) = 2*2 – 4 = 0$. Is it possible to place any more than two “friendly” pawns in the tile $T$? No, because each cell in the first row attacks the diagonal cell in the second row, so you can choose at most one pawn from each “attack pair”. This means that for any unguarded pawn position $\Phi$ on the $2 \times 2$ board, its linear density is bounded by $\Lambda_2(\Phi) \le 0$.

So now what about the 2-linear density for the $n \times n$ board $B_n$? Note that if $n$ is divisible by two we can completely fill up the entire board with these 2-tiles, like this:

Now note that since this n-board (for $n$ = 2k even) is the disjoint union of these $2 \times 2$ tiles $T_1, T_2, …T_{k^2}$, then for any unguarded position $\Phi \in \mathscr{U}(n,P)$, its 2-linear density must be the sum of the densities of these tiles (this follows from Lemma 1) But the positions on those tiles must themselves be unguarded positions, and so for each tile, $\Lambda_2 \le 0$. Therefore, we must have that:

$$\Lambda_2(\Phi) = \Lambda_2(T_1) + … + \Lambda_2(T_{k^2}) \le 0 $$

since all of the terms are known to be $\le 0$. Note that we have also shown that the maximum value of 0 can be attained.

We have just shown that for all even n, and unguarded positions $\Phi$ on the n-board, the value of $\Lambda_2(\Phi)$ is bounded by 0. What about odd n, where $n = 2k+1$? In that case, we can break up the n-board into the disjoint union of $k^2$ tiles which are $2 \times 2$, $k$ tiles which are $1 \times 2$, $k$ tiles which are $2 \times 1$, plus a $1 \times 1$ square, like this:

So now we can play the same game here, and compute the largest possible values of $\Lambda_2$ for each of these little blocks. For both the 1×2 and 2×1 tiles, we have no attack-pairs, and so we can fill both squares with pawns, giving them a maximal 2-density of $\Lambda_2 = 2*2 -2 = 2$. Similarly, we can fill the single 1×1 square with a pawn, for a 2-density of $\Lambda_2 = 2*1 -1 = 1$.

Now there are $k$ of each of the 1×2’s and 2×1’s, and $k^2$ of the 2×2’s and so altogether we can bound the 2-density of the odd n-Board by the sum of these bounds, ie

$$\Lambda_2(\Phi) = k^2 \Lambda_2(2×2) + k\Lambda_2(1×2) + k\Lambda_2(2×1) + \Lambda_2(1×1)$$

$$ \le k^2*0 + k * 2  + k * 2 + 1 $$

$$ \le 4k + 1 \le 4k + 2 $$

$$ \le 2 * (2k + 1) \le 2n $$

And so, what all this means is that for the Pawns, given any unguarded position $\Phi$ on any n-Board, we can bound the largest possible value for its 2-density with a value of C=2, ie,  $\Lambda_2(\Phi) \le 2n$. This proves part (2.1).

Similarly, for the King, we can play the same game, but now using the 4-density $\Lambda_4$. In this case, we can only place one king on the 2×2 tile (since each corner attacks all the others, forming an “attack quadruple”). This gives the 2×2 tile the maximal 4-density of $\Lambda_4 = 4*1 – 4 = 0$. And in the same way, we can show that for even n, the 4-density is bounded by 0, and for the odd case where $n=2k+1$, we can place one king each on the 1×2 and 2×1’s (for a density of $4*1 – 2 = 2$), and one king on the single cell (for a density of $4*1 -1 = 3$). Putting it all together, the King’s 4-density on the odd n-board is given by

$$\Lambda_4(\Phi) = k^2 \Lambda_4(2×2) + k\Lambda_4(1×2) + k\Lambda_4(2×1) + \Lambda_4(1×1)$$

$$ \le k^2*0 + k * 2  + k * 2 + 3 $$

$$ \le 4k + 3 \le 6k + 3 $$

$$ \le 3 * (2k + 1) \le 3n $$

And so for the King we can use the constant $C=3$, so $\Lambda(\Phi) \le 3n$.  This proves (2.3).

Finally, for the Knight, we have to work a bit harder. The Control Area around the knight extends beyond just a single square, and so we need to use a 4×4 tile to build up a solution. In the 4×4 tile we showed above, we were able to fill exactly half (8) with friendly knights, giving the 4×4 tile a 2-density of $\Lambda_2 = 2*8 – 16 = 0$, just like the Pawn. To prove that this is the best we can do with the 4×4 tile and knights, consider the following “attack pairs” of knights on the tile:

We see that there are eight pairs of mutually-attacking squares by knight moves, meaning we can choose at most one from each pair on which to put a knight. This means there can be at most eight friendly knights on any 4×4 tile. And so, just as with pawns we have $\Lambda_2 \le 0$ on any 4×4 tile.

By the same arguments we gave before, if $n$ is divisible by 4, then we can show that an unguarded knight position on an n-board has density $\Lambda_2 \le 0$, and for all other $n = 4j + k$, with $k \le 3$, we can cover the n-board by $j^2$ 4×4 tiles, $2j$ tiles on the border of size $k \times 4$, which can be shown to never have 2-linear densities greater than $\Lambda_2 = 4$, plus a $k \times k$ corner tile, with density no greater than 1. Putting this altogether, it can be shown that a value of $C=1$ is good enough for knights to bound $\Lambda_2(\Phi) \le C*n$ for any unguarded $\Phi \in \mathscr{U}(n, N)$. This proves inequality (2.2) and the Lemma.

$\blacksquare$

PROOF OF THEOREM 1

The theorem is in three parts, for the Pawn, Knight, and King. We will only show the proof for the Pawn, the other proofs are identical in structure. From Lemma 2, formula (2.1), there is a positive constant C such that for all positive integers $n$ and maximally unguarded Pawn positions $\Phi$ on the n-Board, we have

$$ 0 \le \Lambda_2(\Phi) <  C * n$$

which by definition of $\Lambda_2$ means that

$$ 0 \le 2*\Vert \Phi \Vert – \vert \Phi \vert < C*n $$

Dividing both sides by $\vert \Phi \vert$ we have

$$  0 \le \frac{2*\Vert \Phi \Vert}{\vert \Phi \vert} – 1 < \frac{C*n}{\vert \Phi \vert}$$

But since on the n-Board $\vert \Phi \vert = n^2$, we can use the definition of the position density $\delta(\Phi)$ to obtain

$$ 0\le 2\delta(\Phi) – 1 < C/n$$

in other words (adding one and dividing by 2):

$$ \frac{1}{2} \le \delta(\Phi) < \frac{1}{2} + C/2n$$

And so, since $C$ is a positive constant, as $n$ goes to infinity, the value of $C/2n$ becomes vanishingly small, and in the limit goes to zero. By the definition of the asymptotic density, then, the value of $\delta(Pawn)$ is exactly 1/2, which was to be proved.

$\blacksquare$

Unguarded Positions on the Infinite Board

So far, we have been talking about the density of unguarded positions on large but finite boards $B_n$, and their limit as $n \to \infty$ (“n goes to infinity”). But what happens when $n$ gets there? Is there a position on the infinite board $B_\omega$ that is still “unguarded”, and what do we mean by “maximal”?

If we use the finite solutions as a guide, we can quickly propose positions $\Phi_p$ on $B_\omega$ for p = Pawn, Knight, and King. Recall that a “position” on any board B is simply a function mapping every element $(x,y) \in B$ to a member of $\mathscr{P}$, the set of all chess pieces including the “empty” piece $\varnothing$. The omega board consists of all integer pairs $(x,y)$ such that x and y are greater than or equal to zero (so, the bottom left corner square is $(0,0)$).

The solutions are:

$$\Phi_P(x,y)=
\begin{cases}
P, & \text{if $y$ is even} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{Pawn}
$$

 

$$\Phi_N(x,y)=
\begin{cases}
N, & \text{if $(x+y)$ is even} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{Knight}
$$

 

$$\Phi_K(x,y)=
\begin{cases}
K, & \text{if $x$ is even AND $y$ is even} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{King}
$$

It is relatively straightforward to see that when restricted to a finite n-Board these positions are the same as the ones using the “tiles” we defined above, and so they are still unguarded positions. But in what sense are they “maximal”? The weight of these positions are infinite, so how can one infinite position have a greater weight than another? The answer is, they are maximal in that expanding the position to include additional pieces in locations where the original position does not, must also have a hostile piece in the set.

The proof that these positions are indeed maximal, is left as an exercise to the reader.

What the infinite solutions look like

Here are the Knight and King Positions for the infinite boards, as viewed from a great distance (the white squares are the empty ones):

 

 

 

 

 

 

 

 

 

 

This is not actually an infinite board, of course, but a 300 x 300 one. As you can see, as the number of squares on a side increases to infinity, the individual pieces blur out to form a shade of grey, about 50% black for the Knight, and 25% black for the King. Another way to define the density, is that if you were to throw a dart at one of the boards (say, the King), the odds would be 1/4 that your dart would hit a King.

In the next post, we will look at the Bishops, Rooks, and Queens, and see just how strange and different the situation becomes, especially as we venture into larger transfinite boards.

Part II of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

This is part II of my series of blog pieces on a mathematical chess problem. In part one I tried to keep the math to a minimum, but after looking back at the post I see that it may still be a bit too much, and in the next couple of posts the math is only going to get more dense, but there is not much I can do about it.

So for this post I decided to give you a breather, and talk a bit about what the point of all this is.

After digging through my phone I just realized that it has been eight months since I was in the doctor’s waiting room, staring up at the ceiling, and visualizing an infinite chess board with chess pieces sitting on it, none of which were under attack. I took a photo of the ceiling with my phone and included it in my previous post. The date was May 15, 2019.

That fact surprised me; I was sure it was only a few weeks ago that I started scribbling little chess positions on scraps of paper, making notes for a blog post or maybe an article in the American Mathematical Monthly. Gigi’s family will tell you I spent much of the Christmas holiday sitting in a chair, with scraps of paper filled with diagrams and chess boards and incomprehensible hieroglyphics.

What appears to be the case is that this question, of how to fit pawns or queens on an infinite board without attack, spun off numerous other questions and math problems, and some of them were tricky, and some led to questions that seemed difficult. And in the process of thinking about these problems I became lost in a sort of reverie, and lost track of time. Days turned to Weeks turned to months. Eventually I found easy ways to answer many of the problems, and later posts will show those results. But you should realize that it took many tries before I found what now seems to be the obvious approach.

One of the problems was hard enough that I felt that I would need to just leave it in the article is as a conjecture, and hope that somebody smarter than me would be able to solve it.

But just this past Sunday, while out on a training run for the Zion Half Marathon, I came up with a way to solve the problem, and within an hour after getting home I was able to write QED at the end of a proof. Now it too seems obvious, but even so might have made a good Putnam math problem.

In any case, here is the thing. There is a reason why there are all these math symbols and arrows. Each symbol has a precise meaning, and in order to solve a problem it is often the case that the hard part is figuring out how to state the problem in a clear and precise manner. In writing down the math, you are creating a machine, and once done the machine can do a lot of the heavy lifting.

And here is the other thing: why do I do this? Because, believe it or not, it’s fun.

Here’s another preview:

 

First part of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

A while ago I was in the waiting room of the doctor’s office, staring at the ceiling, and looking for something to keep myself amused before the appointment. (The visit was nothing serious, just wanting to update my vaccinations.)

The ceiling was covered with those white acoustic panels, forming a very large colorless and seemingly infinite chess board. I stared at the tiles, trying to think up some kind of puzzle to keep me amused while waiting. I came up with this:

The Chess Density Problem

Suppose you have an infinite chessboard, and an infinite number of one of the six kinds of chess pieces (King, Queen, Rook, Bishop, Knight, and Pawn). What is the densest packing of “friendly” pieces you can have on that board?

Just asking the question raises more questions:

• What do I mean by “infinite” ?
• What do I mean by “densest” ?
• What do I mean by “friendly” ?
• And how would one prove such things?

So far I’ve spend a fair amount of time and scratch paper on this — quite a bit while sitting around with Gigi’s family for Christmas — and have some things to report. The first version of this post was very math-heavy. Now it is a bit lighter. You’re welcome.

Disclaimer

Friends who have suffered through games with me will tell you that I am terrible at playing chess, and spend far too long to come up with a bad move that in standard chess notation would probably be denoted “Nf3 Nc6??”. Not just Chess, but Go, Twixt, Bridge or other strategic games. In defense, I can only say that I am spending all of that time trying to solve the problem, based on the game-theoretic fact that a “best” move exists. The decision tree is so deep, however, that no computer yet exists that can explore it completely more than a few moves ahead.

Good chess players acquire skill through experience and study, making decisions with imperfect knowledge. They stand at the edge of the Grand Canyon of moves and can walk down trails blazed by others. I can only stand at the edge, frozen by the awesome infinitude of the depths. Then I fall in.

Anyway, this isn’t the organic chemistry of Chess, but the simpler math of atoms and fundamental particles, Boards and pieces. Moving on…

Density: A Simple Example

Here is a simple (finite) example of four Queens on a $4 \times 4$ board, where no Queen is attacking any other, either on rank, file, or either diagonal:

 

So for the $4 \times 4$ board, with its 16 squares, you can only “pack” at most four queens, meaning the “density” (which I denote $\delta$) of Queens on this board is

$$\delta = 4/16 = 1/4$$

Is this the “best” we can do in this case? The answer is yes, for the simple reason that at most one Queen can be on each row (or they would not be friendly), and there are four rows.

What is Already Known

This “packing” puzzle is what’s known as a Mathematical Chess Problem, and falls in the category of “recreational mathematics”. That is, mathematics done for amusement rather than “professional” work on “serious” problems. It should be noted, however, that often these problems lead to questions which are actually “deep” and lead to more important work.

In any case, from the literature, the task of arranging “friendly” chess pieces is called an Independence Problem (or an “Unguard” problem), and a chess position in which all of the pieces are friendly is called “Unguarded”. If an unguarded position is the “best” we can do (ie, there is no unguarded position with more pieces), we will call it maximally unguarded.

So, for example, on the standard $8 \times 8$ chessboard, here are examples of how to arrange “friendly” Pawns, Knights and Kings:

 

 

 

 

 

 

 

We will show (later) that these are “maximally unguarded” positions, and so the density of these pieces on the standard 8-board are 1/2, 1/2, and 1/4, respectively.

And here is how to arrange the remaining three “friendly” pieces, the Rooks, Bishops and Queens:

 

 

 

 

 

 

 

These last three are maximally unguarded positions, and so the density for these three pieces on the standard board are 1/8, 7/32, and 1/8, respectively.

To see this in the case of the Rooks and the Queens, we can use the same argument as we did above with the Queens on the 4-board, by noting that there are exactly 8 rows and only one Rook or Queen can be on any row.

For the 14 Bishops, you can make a similar argument, by noting two things:

1. There are exactly 15 diagonals in one direction (shown below in blue), and
2. For each diagonal numbered 1 and 15, there is only one square available for placing a Bishop, and those two squares are “hostile” along the red diagonal, so you can only choose one.

We have separated out the pieces into these two sets of three, because each set have their own unique characteristics, unlike the other set; and the differences in density become more pronounced as the size of the boards becomes larger and becomes infinite. Not only that, but the kind of “density” has to be defined differently, and even the size of the “infinite” board becomes important; as we’ll see, some chess boards are more infinite than others.

Chess Boards: Finite and Infinite

All of the “chess boards” we will be working with will be two-dimensional, and each “square” on which a chess piece can be placed can be indicated by a pair of numbers $(x,y)$, where $x$ and $y$ are coordinates in some set $A$, which we will call the Address space. A chess board that uses coordinates in Address space $A$ will be denoted $B_A$. Mathematically, the board $B_A$ can be identified with the Cartesian product $A \times A$.

For example, the squares of our standard $8 \times 8$ chess board can be specified using $A = \{0,1,2,3,4,5,6,7\}$. The set of integers from 0 to 7 is sometimes denoted $\mathbb{Z}_8$, and so the standard chess board is $B_{\mathbb{Z}_8}$.  To make life simple(r), we will also call this board $B_8$, or simply the “8-Board”, and similarly an $n \times n$ board (where n is an integer) will be called the “n-Board”, or $B_n$.

Here for example is the 5-board $B_5 = B_{\mathbb{Z}_5}$:

Okay, so far so good (you still with me, here?). Now the point of all this mathematical gobbledegook (a scientific term), is that I wanted to look at the “Unguarded” chess problem on an infinite chess board, meaning that I want to use for a “coordinate space” $A$ an infinite set. The first one that comes to mind is the set of whole numbers, ie

$$\mathbb{W} = \{0,1,2,. . .\}$$

And so we can define our first infinite chess board as $B_{\mathbb{W}}$, consisting of all $(x,y)$ where $x$ and $y$ are non-negative integers.

Intuitively, the board can be visualized like this:

This picture looks a lot like the ceiling at my doctor’s office, which is what started this whole thing.

Now the “size” (cardinality) of the whole numbers is “infinite”, but the specific mathematical name for this “infinite” value is $\aleph_0$ (pronounced aleph-null). Unlike the conventional symbol for infinity ($\infty$), $\aleph_0$ has a more precise meaning, and it refers only to “countably” infinite sets, ie, those which you can count with the integers 1,2,3, etc. A related infinite “ordinal” number is called $\omega$ (small omega), and with some “abuse of notation” we will refer to $B_{\mathbb{W}}$ as $B_{\mathbb{\omega}}$, or simply the $\omega\text{-Board}$.

Chess Boards: Infinity and Beyond

There are many other ways to define infinite boards, but for now the only other board we will look at uses as its coordinate space the closed unit interval on the real line, that is,

$$I = \{ x \in \mathbb{R}: 0 \le x \le 1 \}$$

The board $B_I$ can be visualized as the unit square, including every single point on the boundary and in the interior as a distinct “square” on which you could place a chess piece:

 

 

 

 

 

 

 

 

The size of the set of real numbers in $I$ is a transfinite number which is infinitely larger than $\aleph_0$, and is called simply $c$, the infinity of the continuum. If we embrace “The Continuum Hypothesis“, this number c can be identified as $\aleph_1$, the next largest infinity. We shall therefore also call $B_I$ the c-Board, or $B_c$. The number of “squares” on $B_c$, unlike the $\omega\text{-Board}$, is uncountably infinite.

Sneak Preview

The “density” results for each infinite board and piece will be shown (in later posts) to be as follows.
The pieces are in order of their decreasing (2d or fractal) density, and thus their increasing “power”:

$$\omega\text{-Board}$$

Piece	Board	2d-Density	Fractal Dimension	1d-Measure (**)
Pawn	$B_\omega$	1/2	2	*
Knight	$B_\omega$	1/2	2	*
King	$B_\omega$	1/4	2	*
Rook	$B_\omega$	0	*	*
Bishop	$B_\omega$	0	*	*
Queen	$B_\omega$	0	*	*

$$c\text{-Board}$$

Piece	Board	2d-Density	Fractal Dimension	1d-Measure (**)
Pawn	$B_c$	*	*	*
Knight	$B_c$	*	*	*
King	$B_c$	*	*	*
Bishop	$B_c$	$0$	$1$	$2\sqrt 2$
Rook	$B_c$	$0$	$1$	$2$
Queen	$B_c$	$0$	?	?

(*) Not Defined for this piece on this board.

(?) Unknown whether a Hausdorff-measurable solution exists.

(**) 1d-Measure = (Hausdorff Content)

As you can see from the two tables, there is something very different between the two groups of pieces, and how they “pack” on those infinite boards. In following posts, I will try to explain what the differences are, what a Fractal Dimension is, and what other mathematical issues and questions arise in the process.

 

 

 

 

I’ll make this (mercifully) short.

Consider this statement, which I call Ω:

Everything travels through the Cosmos at exactly the speed of light.

Ω is Relativity. That’s it. Really, it is. And Ω is true not only for Special Relativity, but the General one too. All you have to know is that the “Cosmos” means both space and time.

If you were to ask somebody what Relativity says, they would probably say something like “everything is relative.” The problem with that is, it’s not precise. In fact, it’s not even true. Some things in physics (and the world) are thought to be absolute. So I’ve been trying to come up with a good version of Relativity that can be justified mathematically, and that little box is what I came up with. If you understand what each word means exactly, everything follows from this statement, and if you like you can stop reading now and get on with life. Because that really is what relativity says.

The rest of this short post is just me rambling about why I like it. In a later post I’ll defend it. Also, here is a cool picture of a galaxy for no reason. But it’s cool (*).

Why I like This Version of Relativity

One of the things I like about this version (Ω) is that it is simple and precise, sounds a little strange — but just enough strange to be right — and answers immediately a number of other questions people ask about relativity, matter, speeds etc. For example:

Q: Will we ever be able to go faster than light?

A: NO. The reason you can’t go faster than the speed of light is that you can’t go any slower either. Nothing in the universe can go any speed in spacetime but c, the speed of light. The only thing you can ever change is the direction in space-time that you are going.

Q: Why does Relativity say that when you go faster, time slows down?

A: Because you are always going exactly at the speed c, so if you go faster in the space directions, you have to go slower in the time direction so it still adds up to exactly c.

See?  Details later, film (and math) at 11. But really, it is true. Ask a physicist. He’ll scratch his head, then say yeah, that works, then go have a beer.

(*) Photo: Centaurus A, (Image Credit: X-ray: NASA/CXC/CfA/R.Kraft et al.; Submillimeter: MPIfR/ESO/APEX/A.Weiss et al.; Optical: ESO/WFI)