A Chess Puzzle, Part VI: The Bishop

Part VI of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

We are now approaching the end of the story, with the final tale of the Fractal Queen approaching. But for now we must deal with with the Bishop, a close cousin to the Rook.

Recall that our puzzle revolves around the maximum “unguarded” positions of a chess piece on a board; in this case Bishops. In some sense, the Bishop can be thought of a Rook turned sideways, because both pieces can only move in two orthogonal directions, but the Bishop’s directions are along the 45 degree diagonals. The difference this makes though is that Bishops have a “color” while Rooks do not. Rooks can move to any square on the board while a Bishop on black squares can only attack other black squares.

This limited ability to only attack half of the squares that a Rook can, makes Bishops slightly “weaker”, and so it should not be surprise (as we showed in part I), that on an $n \times n$ board, we can place $2n – 2$ Bishops, giving them a density of roughly $\frac{2}{n}$ for large $n$, and asymptotically going to zero on the infinite board. So in some sense the friendly Bishop’s density on the board is roughly twice that of the slightly more powerful Rook.

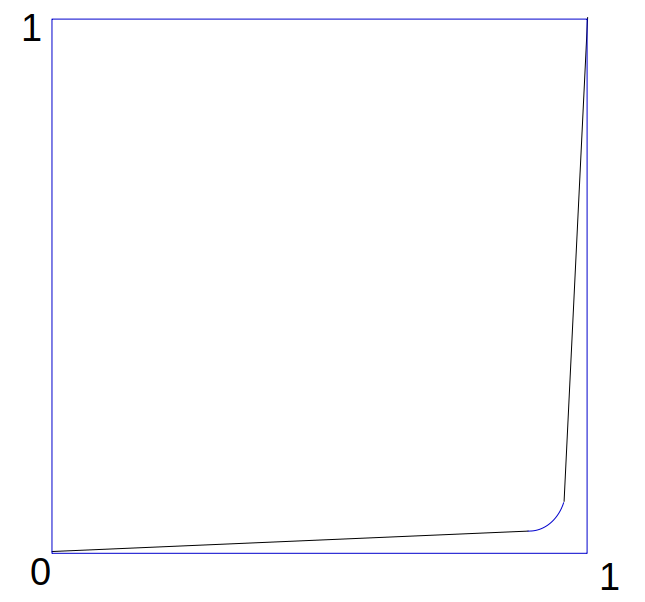
But as with the rook, this is the two-dimensional density, while the unguarded Bishop positions clearly have a fractal dimension of one on the board. And as we saw with the Rook, once we go to the unit square board $\mathbb{B}_I$, with a continuum of “squares” at each real coordinate, the rigid shape of the solutions can loosen, so that instead of just the diagonal set with linear measure of $\sqrt{2}$ we can have a set of “friendly” Rooks on the board with 1-dimensional content of nearly 2:

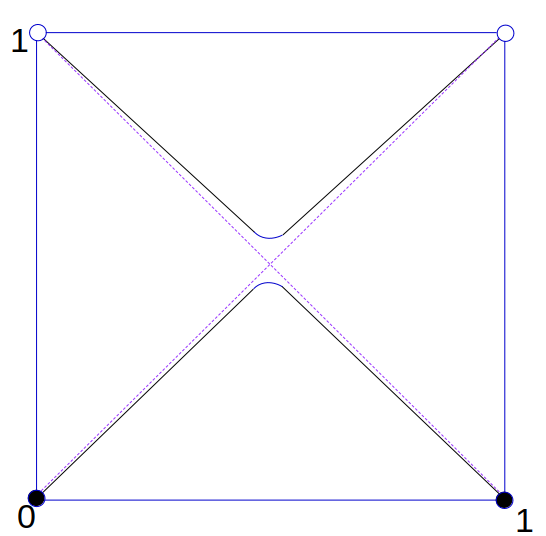
and so, turning everything “sideways”, we can see that instead of a set of Bishops on the top and bottom row of the board with measure 2, we can stretch them toward each other, approaching a linear measure of almost $2\sqrt{2}$:

(Note that we have placed black and white circles in the corners to indicate that only the bottom corners are occupied with Bishops, which are in turn attacking the top corner locations). Again, as with the Rook solutions, there are no analogous version of these “continuum” solutions in the finite/discrete boards, as their topology is not dense.

Now one would think that the remaining piece — the Queen — would not be much different from the Rook or Bishop, as it simply has the capturing power of both. But as we will see, the problem suddenly become *very* different, and goes into some very deep and fascinating mathematics on the infinite boards.