A Chess Puzzle, Part VIII Conclusion: The Transfinite Super Queen and Beyond

Final Conclusion of the journey of A Mathematical Chess Puzzle:
- Part I: The Infinite Chess Board
- Part II: Ruminations
- Part III: The Pawns, Knights and Kings
- Part IV: A Group of Rooks
- Part V: Rooks and Topology
- Part VI: The Bishop
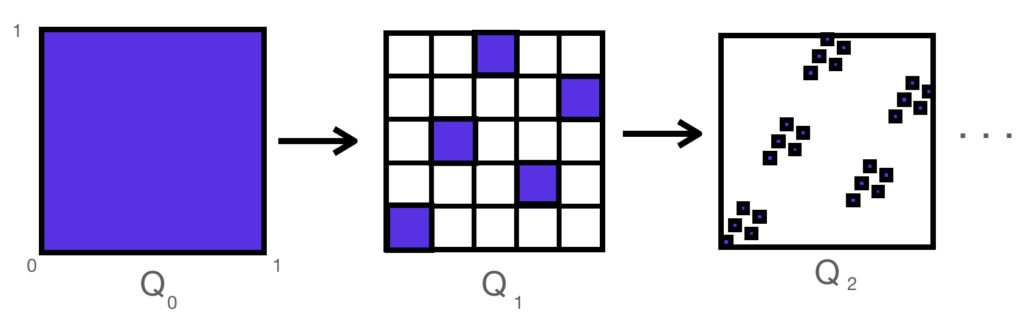
- Part VII Episode 1: The Fractal Queen
- Part VII Episode 2: The Rational Super Queen
- Part VIII Conclusion: The Transfinite Super Queen and Beyond
Journey’s End
It has been a long journey, but with this post the story of the Mathematical Chess Puzzle will be coming to an end.
When I first sat down in the waiting room at Southern Utah’s Intermountain Health Care on May 19, 2019, and stared up at the infinite array of square acoustic tiles in the ceiling, the 2020 election was still over a year away. There was no worldwide pandemic that had killed off a million people worldwide and affected a third of everybody I knew. The company I had worked at since 1995 was still my employer. The company I worked for next did not yet even exist. Our best friend in town had not yet died tragically of a stroke. Her cats who had been rendered homeless had not come to live with us. There was no Russian invasion and war with Ukraine. There was no attempted overthrow of the US government. There were no Llamas in our back yard named Dewi and Karl, clearing out weeds. My wife had not yet been convinced to run and then win the race to become Mayor of the town of Virgin. And up until today (June 12 2022), my wife had not contracted Covid. She’s doing ok.
Yet through all of this, and more, I would steal time from work, and grab some blank paper, and sketch some chess positions, look up articles, refresh my knowledge of group theory and work on each chess piece, to understand both its power and its “density” as a result of that power.
We would travel to Gigi’s siblings houses in Austin Texas, I would lie on the couch, and scribble some more diagrams, then go to Chuy’s restaurant, still thinking about the problems, hoping to remember some flash of insight about the Rook, through all the margaritas I had just drank.
This last leg of the journey was the longest. In my line of mathematics I had not heard of Transfinite Induction, and the bizarre amazing results that could be proven with it (as sensible as the Axiom of Choice may seem). It was not at all clear to me at the beginning that I would be able to solve this problem, but yet I did.
Let us then begin the end at the beginning, with the story of Numbers. This story is going to go to some strange places, but to end the story, we have to go there. So humor me …
Numbers, Ordinal and Cardinal
In order to attack the Super Queen Theorem, we will need to make use of the properties of ordinal and cardinal numbers. Most folks understand on some level the difference between these two. Cardinal numbers simply say how many things there are, while Ordinal numbers pay much closer attention to the order – of which ones come first. In other words, it is the difference between five sheep and the fifth sheep (or the sixth sick sheikh’s sixth sheep — which I hear is ailing). So the Cardinal numbers go Zero, One, Two Three, while the Cardinal numbers go Zeroth, First, Second, Third.
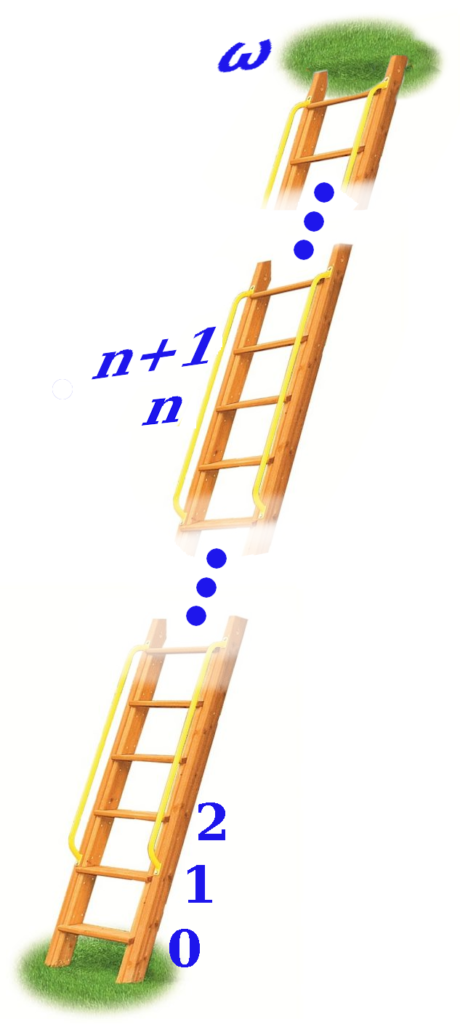
Things however become much more complex (and possibly confusing) once you start dealing with infinite sets of things. For example, if you consider the set of Whole numbers $\mathbb{W} = \{0, 1, 2, …\}$, the members have the property that they are ordered, and that if m and n are distinct elements, then either m > n or n > m. Now suppose you create a new set $\mathbb{W}^*$, which is all of the elements of $\mathbb{W}$, together with a new member called $\omega$ (omega), for which it is understood that $\omega > n$ for all whole numbers $n$. You can then define addition on this new set, with numbers like $\omega + 1$, $\omega + \omega = 2\omega$ and so on. It turns out that each of these are good *ordinal* numbers and you can always define the “>” operator in a consistent way. But even with all these new ordinals, it turns out that in terms of the *size* of these new sets, they both have the same number of elements, which is $\aleph_0$. It is only when you extend the whole numbers to real numbers, that suddenly the cardinality increases, to $c$, the cardinality of the continuum, which is strictly greater than $\aleph_0$.
Note: for a good expository article on transfinite induction and its uses, see Sylvia Durian’s article, “Some Transfinite Induction Deductions“, which was part of the University of Chigago Math department’s “Research Experience for Undergraduate” (REU) program.
Transfinite Induction
The relationship between ordinal numbers and (regular) mathematical induction is fairly clear. In order to prove some statement S(n) for all whole numbers n, you first prove S(0), and then prove that if S is true for the nth value, then it is true for the (n+1)th value. In other words, you have to prove the statements in order, and from there you can go to $\omega$.
The idea for transfinite induction is basically the same, except that you are iterating not just on finite $n$ steps, but on steps $\alpha$, where $\alpha$ may be an ordinal which is already itself infinite.
Because of the delicate nature of this transfinite arithmetic, the way in which “mathematical induction” must be extended to such numbers must be handled differently. In order to do this, we have to distinguish between different kinds of “ordinal” numbers, some finite, some infinite, and some more infinite than others such as $\omega^2, \omega^\omega$, etc. See the diagram below.
Successor Ordinals and Limit Ordinals
So consider our extended “Whole” numbers $\mathbb{W}^*$ above where we have added a new “infinite” number $\omega$, whose property is that it is greater than all finite whole numbers. The number $\omega$ is different from the finite ones in an important way: given any positive finite ordinal $n$, it has a predecessor, $n-1$ as well as a successor $n+1$. Unlike these, the number $\omega$ has no immediate predecessor, though it does have successors $\omega +1, \omega+2$ etc. Ordinals with no predecessors are called limit ordinals. Ordinals which do have predecessors are called successor ordinals. By this definition, note also that the first whole number $0$ is a limit ordinal.
The Principle of Transfinite Induction
In order to prove statement $S(\alpha)$ for all $\alpha$ in some infinite index space $\Lambda$, you must prove not two but three things (see wikipedia):
- Zero Case: Prove that $S(0)$ is true
- Successor case: Prove that for any successor ordinal $\alpha +1 \in \Lambda$, that $S(\alpha + 1)$ follows from $S(\alpha)$
- Limit case: Prove that for any limit ordinal $\lambda$, $S(\lambda)$ follows from $S(\beta)$ for all $\beta \lt \lambda$.
It is this last step that is the new twist, which we did not have to do in the finite “rational board” case.
We will also need one other important item for our toolkit.
(Ernest) Zermelo’s Theorem: Every set $S$ can be well-ordered. That is, every element in $S$ can be assigned an index or label $\alpha$, and an ordering $\le$ such that $\{ \alpha, \le \}$ is a well ordered set.
These two theorems are well known, and we will not prove them here. The latter is a direct consequence of the Axiom of Choice.
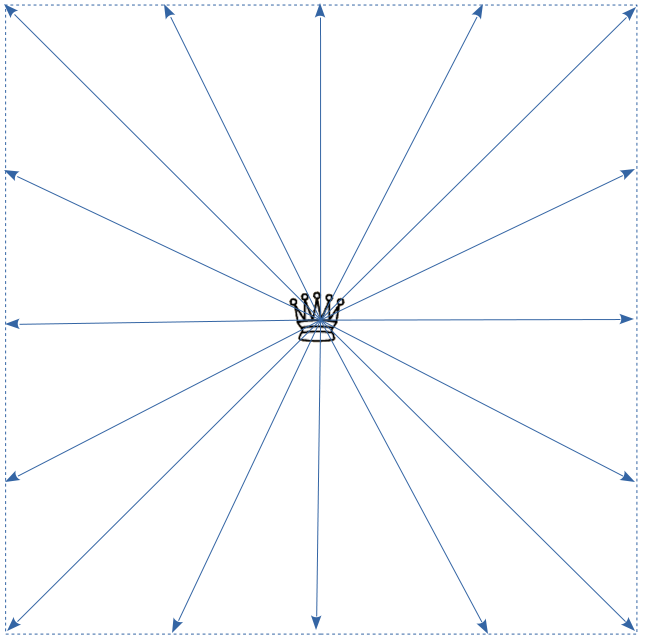
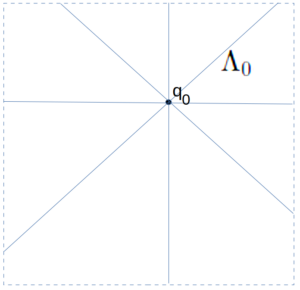
Definition: In any subset $S \subset \mathbb{R}^2$, the queen lines $\Lambda(S)$ of $S$ are the intersection with $S$ of all lines of the form $ax + by = c$, where $(|a|,|b|)$ belongs to the set $\{ (1,0), (0,1), (1,1) \}$ and $c$ is any real number. In other words the queen lines are any horizontal, vertical, or diagonal lines in the plane.
The Transfinite Super Queen Theorem: In the open unit board $\mathbb{B}^* = \mathbb{B}_{I^*}$, where $I^* = (0,1)$, there exists a “position” (set of points) $Q \subset \mathbb{B}^*$ such that every queen line of $\mathbb{B}^*$ meets $Q$ in exactly one point.
PROOF: Let $\Lambda = \Lambda(\mathbb{B}^*)$ be the set of all queen lines $\lambda$ that intersect the unit board $\mathbb{B}^*$, and let $\{ \lambda_{\alpha} \}$ be a well-ordered labeling of that set using ordinals $\alpha$ (which we know exists by Zermelo’s Theorem). We will use transfinite induction on $\alpha$ to construct a sequence $\{ Q_\alpha \}$ of sets $Q_\alpha \subset \mathbb{B}^*$, such that for every $\alpha$, the following properties hold:
i) $Q_\alpha$ contains at most one point.
ii) $\bigcup\limits_{\beta \le \alpha} Q_{\alpha}$ does not contain any pairs of points belonging to the same queen line.
iii) $\bigcup\limits_{\beta \le \alpha} Q_{\alpha}$ contains exactly one point of $\lambda_\alpha$.
Following the principle of Transfinite Induction, we must consider three cases. The Zero Case — to get started, the Successor Case — which gets us to a step having a preceeding step, and the Limit Cases. This latter is the new one, and are those infinitely far away steps where there is no immediate preceeding step, but an infinity of previous ones, even an infinity of infinity of them.
Zero Case: We arbitrarily pick any point $q_0 \in \lambda_0$, and define $Q_0 = \{ q_0 \}$. The three properties (i)-(iii) are seen to hold trivially.
Successor Case: Suppose for successor ordinal $\alpha + 1$ the sequence $\{ Q_\beta\}_{\beta \le \alpha}$ satisfies properties (i)-(iii) for $\alpha$. We must construct (and prove) that there exists a set $Q_{\alpha +1}$ for which those properties also hold.
Consider the set $Q = \bigcup\limits_{\beta \le \alpha} Q_{\alpha}$. By (ii) we know that it does not contain any pairs of points belonging to any queen lines, including $\lambda_{\alpha +1}$. There are therefore just two cases to consider:
Case 1: If $|Q \cap \lambda_{\alpha +1}| = 1$, define $Q_{\alpha + 1} = \emptyset$. This clearly satisfies all three conditions for $\alpha + 1$.
Case 2: if the intersection is empty, define $Q_{\alpha + 1} = \{q\}$, where $q \in \lambda_{\alpha + 1}$ is chosen by the following process:
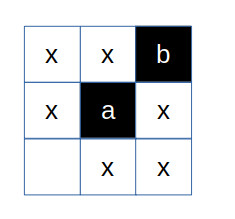
Let $Q = \bigcup\limits_{\beta \le \alpha} Q_{\alpha}$ and define $\Lambda(Q)$, to be the set of all queen lines passing through Q. Now through any point only four distinct queen lines can pass, and so the intersection of $\Lambda(Q)$ with queen line $\lambda_{\alpha + 1}$ has cardinality no more than
$$4*|Q| \lt 2^{\aleph_0} = |\lambda_{\alpha + 1}|$$
in other words, the set
$$\lambda_{\alpha + 1} \setminus \Lambda(Q) \ne \emptyset$$
Hence we can choose $q \in \lambda_{\alpha + 1}$ to be any element in this remaining set, and define $Q_{\alpha +1} = \{q\}$. We assert that this satisfies all three conditions (i)-(iii). This follows immediately by the construction itself.
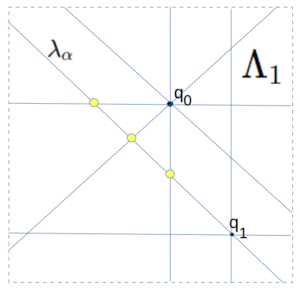
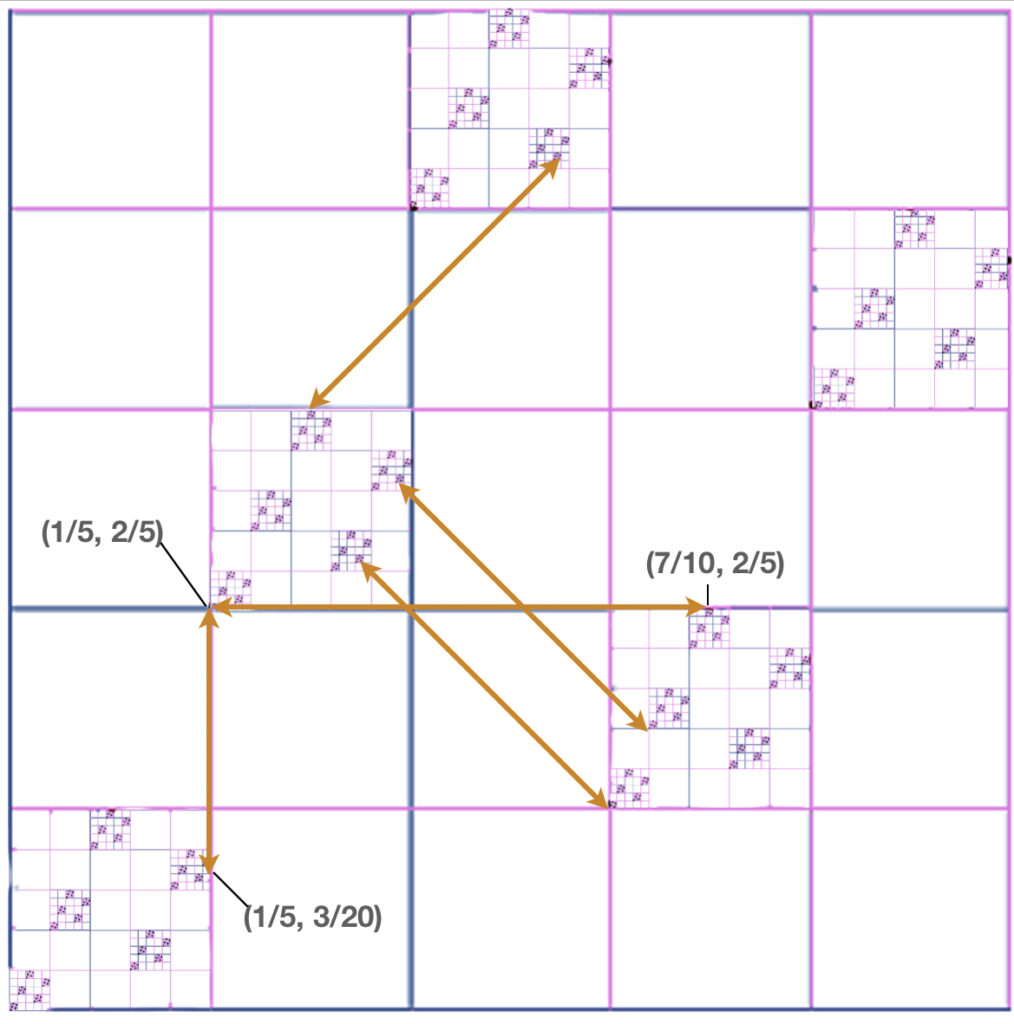
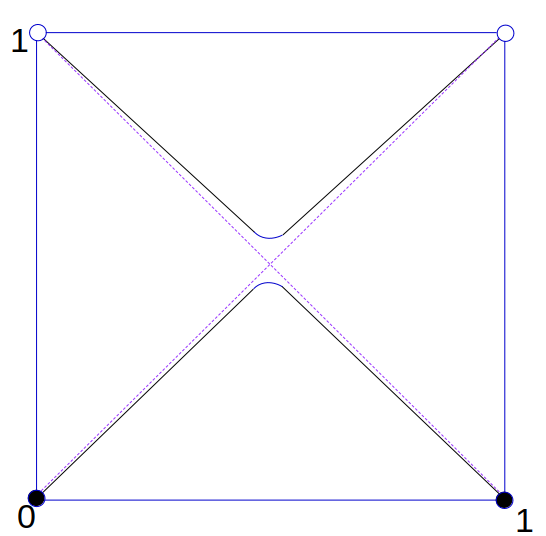
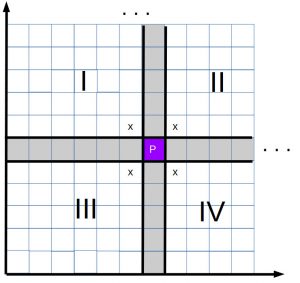
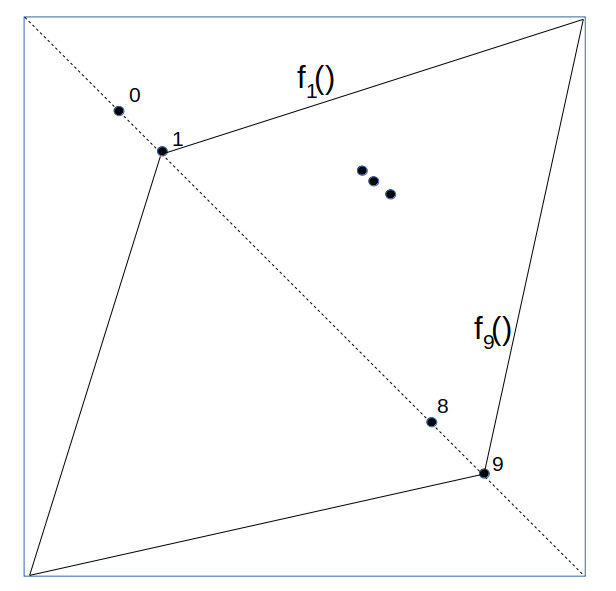
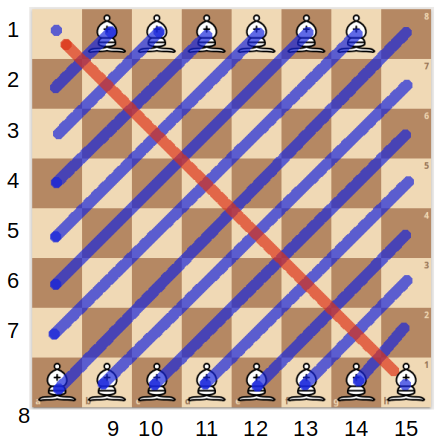
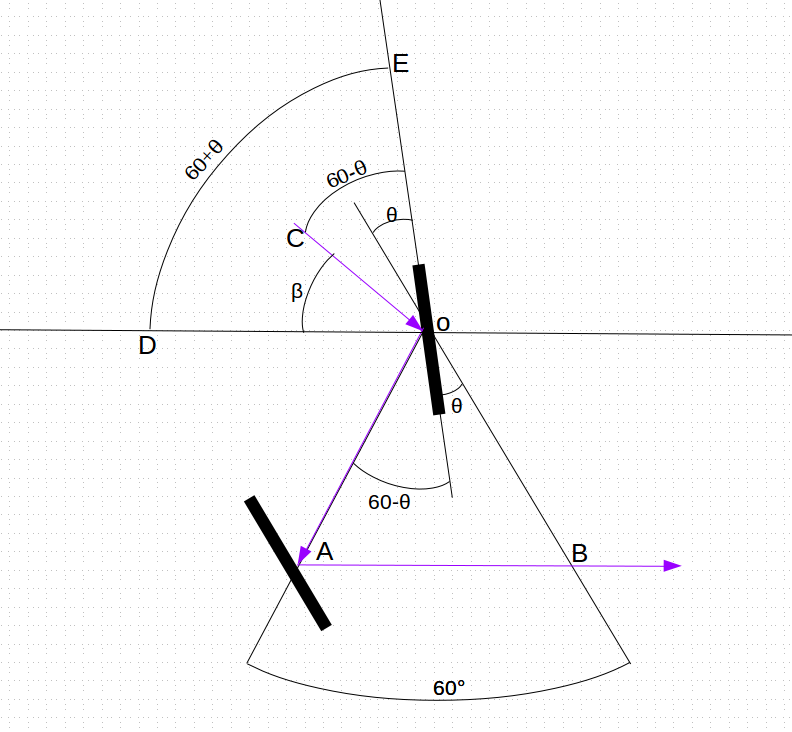
This diagram below may help clarify the rather complex chain of arguments above:
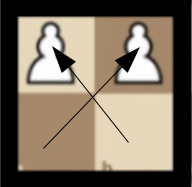
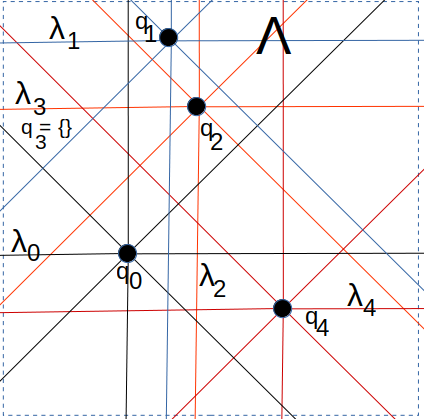 The small lambdas are the successive queen lines in the well-ordered sequence. For line $\lambda_0$ we chose an arbitrary point $q_0$ on it. Inspecting $\lambda_1$ we see it does not intersect $Q = \{q_0\}$ and so we are in Case 2 and we carefully choose $q_1$ to be a point not in the intersection of $\lambda_1$ with any queen lines passing through $q_0$. For $\lambda_2$ we have the same case and again we define $q_2$ to be a point not in the intersection of $\lambda_2$ with any queen lines through $\{q_0, q_1\}$. Moving on to $\lambda_3$, we see that it actually intersects with $q_2$, meaning that we are in Case 1. In this case, we simply define $Q_3 = \{\}$, the empty set, and move on to $\lambda_4$, which is back to Case 2.
The small lambdas are the successive queen lines in the well-ordered sequence. For line $\lambda_0$ we chose an arbitrary point $q_0$ on it. Inspecting $\lambda_1$ we see it does not intersect $Q = \{q_0\}$ and so we are in Case 2 and we carefully choose $q_1$ to be a point not in the intersection of $\lambda_1$ with any queen lines passing through $q_0$. For $\lambda_2$ we have the same case and again we define $q_2$ to be a point not in the intersection of $\lambda_2$ with any queen lines through $\{q_0, q_1\}$. Moving on to $\lambda_3$, we see that it actually intersects with $q_2$, meaning that we are in Case 1. In this case, we simply define $Q_3 = \{\}$, the empty set, and move on to $\lambda_4$, which is back to Case 2.
To finish this proof, however, we still have one more case, which is for limit ordinals (a case which does not occur in finite induction).
Limit Case: We now consider the case where $\alpha$ is a limit ordinal with no immediate predecessor, and where all that we know is that conditions i-iii hold for all ordinals $\beta < \alpha$. We must show that we can find a set $Q_\alpha$ which also satisfies the conditions for $\lambda_\alpha$.
Consider now the collection of nested sets $S_\gamma = \bigcup\limits_{\beta \le \gamma} Q_{\gamma}$, for $\gamma \lt \alpha$. We know that by (ii) none of them contain any pairs of points on the same queen line. We assert that their union
$$Q = \bigcup\limits_{\gamma \lt \alpha} S_{\gamma} = \bigcup\limits_{\beta \lt \alpha} Q_{\gamma}$$
has the same property and contains no pairs of points on any queen line. We will prove this by contradiction. To see this, consider the set $T \subset \Lambda$, defined to be the set of all queen lines (if they exist) for which $Q$ does contain a pair of points as members. As a well-ordered set $T$ must have a member with the lowest index, call it $\lambda_\epsilon$. This queen line is presumed to meet $Q$ in two points, call them $p$ and $q$. As members of $Q$ which are unions of $S_\beta$, these two must be members of two specific $S_\beta$, call them $\beta_p$ and $\beta_q$. Let $\kappa$ be the larger of these two. Since the $S_\gamma$ are nested, this means that both $p$ and $q$ are in $S_\kappa$. But $\kappa \lt \alpha$, and so we know that $S_\kappa$ satisfies condition (ii), a contradiction.
Thus we conclude that $Q$ satisfies (ii) in the sense that it contains no pairs of any queen line. Let us now define $Q_\alpha$ to satisfy (i-iii). We know that $Q$ does not contain a pair of points in $\lambda_\alpha$ and so we have once again two cases:
Case 1: If $|Q \cap \lambda_{\alpha}| = 1$, define $Q_{\alpha} = \emptyset$. This clearly satisfies all three conditions for $\alpha$, as Q clearly contains exactly one element of $\lambda_\alpha$.
Case 2: if the intersection is empty, we shall define $Q_{\alpha} = \{q\}$, where the point $q \in \lambda_{\alpha}$ will chosen by a process similar to the successor case. Once again, let $\Lambda(Q)$ be all queen lines passing through $Q$, and consider the set of all intersections $\Lambda(Q) \cap \lambda_\alpha$. Now the cardinality of $\Lambda(Q)$ (though it may not be finite) is strictly less than $2^{\aleph_0}$. Meanwhile, the points in the queen line $\lambda_\alpha$ can be mapped bijectively to the set $\mathbb{R}$ of real numbers, whose cardinality is exactly $2^{\aleph_0}$. This means, once again, that the set $\lambda_\alpha \setminus \Lambda(Q)$ is nonempty. Let us choose $q$ to be a member of this nonempty set, and define $Q_\alpha = \{ q \}$.
We claim that this set $Q_\alpha$ satisfies (i-iii). As before, this follows directly from the manner in which $Q_\alpha$ was constructed.
We have thus constructed by transfinite induction a family $\{Q_\alpha\}$ which for every $\alpha$ satisfies properties (i-iii). We define position $Q = \bigcup\limits_{\alpha} Q_{\alpha}$, and assert that this set of points meets every queen line in $\Lambda$ at exactly one point. To see this, it is only necessary to see that for each $\alpha$, the queen line $\lambda_\alpha$ meets (by construction) the subset $Q_\alpha$ in exactly one point $p$. And conversely, were this line $\lambda_\alpha$ to meet $Q$ in any other point $q$, then by construction this $q$ must belong to another $Q_\beta$. If we choose $\kappa$ to be the larger of $\alpha$ and $\beta$, we would then see that
$$\bigcup\limits_{\gamma \le \kappa} Q_{\gamma}$$
would have to contain both $p$ and $q$, which are members of the same $\lambda_\alpha$. But this would violate property (ii) for $\kappa$, and contradict the manner in which $Q_\kappa$ was constructed. And so we must conclude that $Q$ only meets $\lambda_\alpha$ in exactly one point, and so $Q$ does indeed satisfy the definition of the Super Queen Position.
QED
A Metaphysical Issue
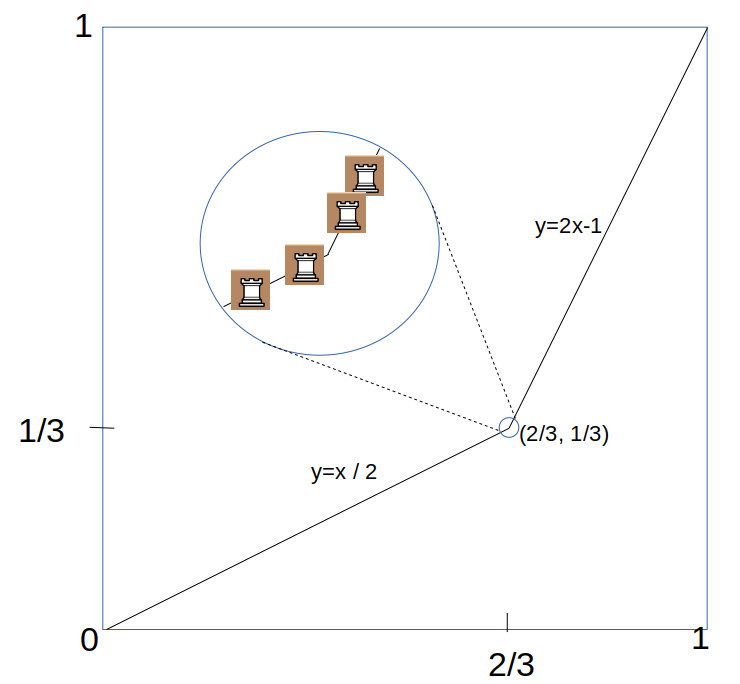
We have just proven by transfinite induction that a “Super Queen” position exists for which every queen line has exactly one queen guarding that line, and therefore no queens attacking each other. As with many theorems proven using transfinite induction, the problem is that even though we know a solution exists, and we have a “construction” for it, we have to make an arbitrary choice, and so we do not have an algorithmic computable constructive proof, such as for the bishops and rooks. Our one attempt at constructing such a solution, the Fractal Queen, proved to fail the conditions once we went to the limiting cases, with queen points converging to conflicting positions elsewhere on the board. As mentioned in that post, I do not know if a solution is constructable. In any case, it is interesting to know that a solution exists.
Epilogue: The Transfinite Hyper Queen
We have just proven through transfinite induction that on the real unit board, there exists a Super Queen Position $Q$, in which every queen line is attacking exactly one square in the position. But can we say more?
For example we have granted the Queen the powers of both the Rook and the Bishop. But what if we also granted a “Hyper Queen” the real-line version of the Knight?
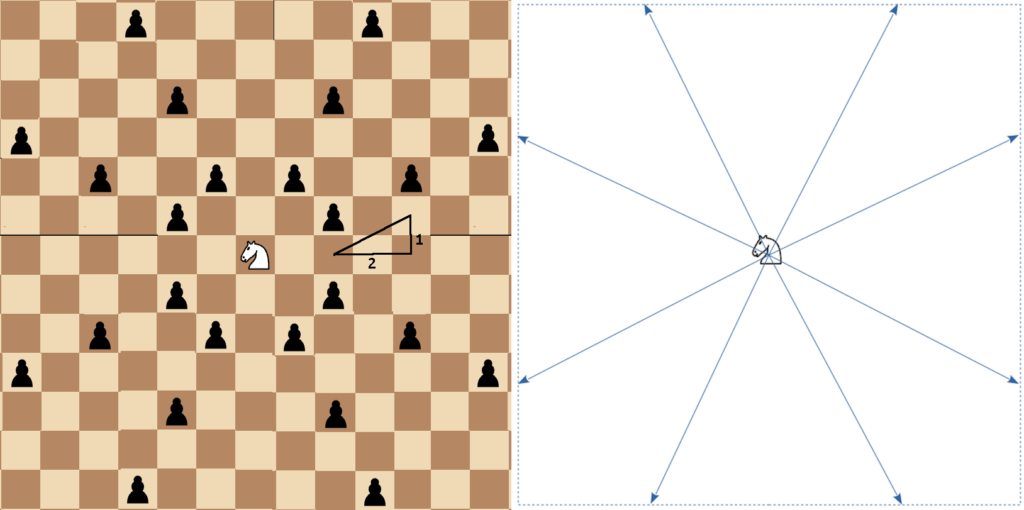
Recall that a classic Knight attacks squares in the diagonals of rectangles that from center-to-center are in ratios of either 1:2 or 2:1. If so, then a “Super Knight” on the real board should be able to attack any point along any line whose slope in absolute value was either 1/2 or 2.
Thus we could define a Hyper Queen like this:
Definition: In any subset $S \subset \mathbb{R}^2$, the hyper-queen lines $\Xi(S)$ of $S$ are the intersection with $S$ of all lines of the form $ax + by = c$, where $(|a|,|b|)$ belongs to the set $\{ (1,0), (0,1), (1,1), (2,1), (1,2) \}$ and $c$ is any real number. In other words the hyper queen lines are any horizontal, vertical, diagonal, or “knight-like” lines in the plane.
Now, if one goes back and looks through the proof of the Super Queen Theorem, we made no distinction between rook or bishop style lines, and only depended upon the manner in which the families of lines intersected each other in finite ways. Thus, by following the exact same argument, it is possible to prove this:
The Transfinite HYPER Queen Theorem: In the open unit board $\mathbb{B}^* = \mathbb{B}_{I^*}$, where $I^* = (0,1)$, there exists a “position” (set of points) $H \subset \mathbb{B}^*$ such that every hyper-queen line of $\mathbb{B}^*$ meets $H$ in exactly one point.
Proof is left as an exercise to the reader.
Final Note at the End
As I write this, it turns out that now (June 18, 2022) I, too, have tested positive for Covid-19. My wife is still doing okay and recovering, and I am taking my medicine as ordered, and am not having many serious symptoms. It is satisfying, knowing that I was able to resolve this mathematical puzzle before life got too … complicated. Stay tuned.