A Chess Puzzle, Part III: The Pawns, Knights and Kings

Part III of A Mathematical Chess Puzzle:

• Part I: The Infinite Chess Board
• Part II: Ruminations
• Part III: The Pawns, Knights and Kings
• Part IV: A Group of Rooks
• Part V: Rooks and Topology
• Part VI: The Bishop
• Part VII Episode 1: The Fractal Queen
• Part VII Episode 2: The Rational Super Queen
• Part VIII Conclusion: The Transfinite Super Queen and Beyond

This is part III of my series of posts on the “Chess Density Problem”. In Part I, I introduced the problem and laid out some definitions to clarify what I meant by some of the terms such as “Board” and “Density”. In Part II I gave everyone a breather.  Hope you’ve rested up. In this one the math is going to be a bit thick, but the purpose of it all will be to prove this first theorem:

The Chess Density Theorem – Pawn, Knight and King

DENSITY THEOREM 1: For Pawns, Knights, and Kings, their asymptotic density $\delta$ on the infinite board ($B_{\omega}$) is given by:

1.1) $\delta(P) = 1/2$.

1.2) $\delta(N) = 1/2$.

1.3) $\delta(K)= 1/4$.

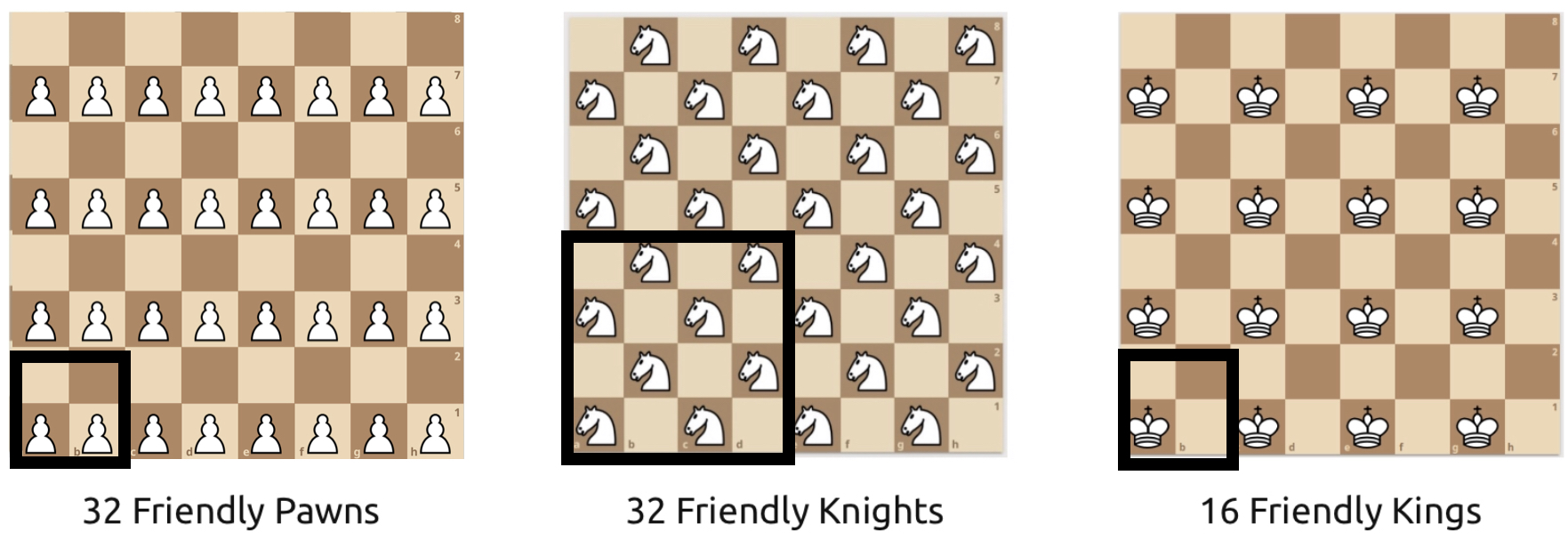
In other words, on an infinite chess board, you can pack at most half of the squares with “friendly” Pawns or friendly Knights, and only a quarter of the board with friendly Kings. As a reminder, by “friendly” I mean that none of the pieces are threatening each other by standard chess rules.

Plan of Attack

As a starting point, we can note that the solutions found on the standard 8-board can be seen as built up from simple “tile” patterns made of identical small boards:

 

These tiles each have the densities that are claimed by the Density Theorem above. If we can prove that no such tiles can have a greater density, we can show that this must hold for larger boards. The way which we will do this is to define a precise way to “measure” the density of any arbitrary block of squares, and prove some useful properties of that measure-function.

Definitions

It always helps to define things precisely. There are a lot of fancy symbols, but the general ideas should be clear.

The Pieces

The six standard Chess pieces are King, Queen, Bishop, Knight, Rook, and Pawn, which we will denote with the initials {K,Q,B,N,R,P}, respectively. To this set we will also add the “Empty” piece, denoted $\varnothing$, which indicates that a square is empty.

The set of all pieces including the empty piece will be denoted

$$\mathscr{P} = \{K,Q,B,N,R,P,\varnothing \}$$

We include that “empty” piece to allow us to explicitly specify that a square is empty.

Control Zones

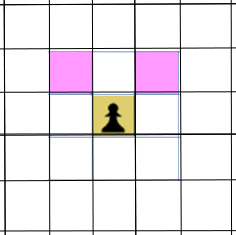
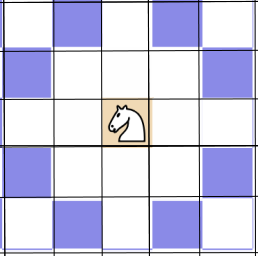
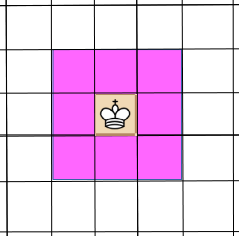
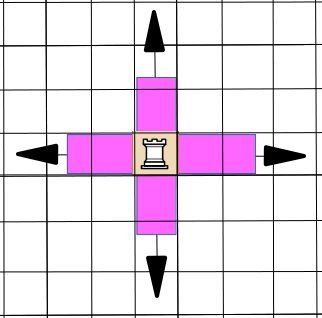
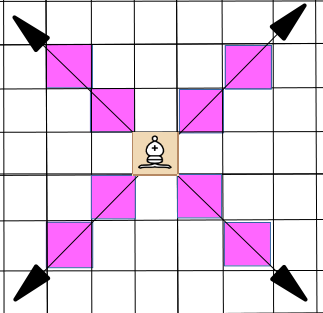
DEFINITION: The control zone of a piece X at position $x$ on a board B is the set of all other locations $y \in B$ which (by the standard rules of chess) are subject to attack by X (with no other pieces on board).

The Control Zones of the Pawn, Knight and King are shown in blue below:

 

 

 

 

 

 

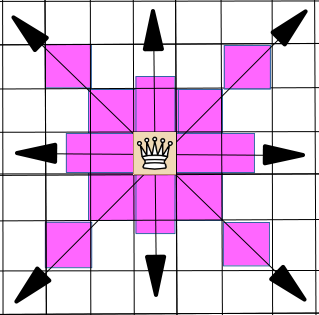
One thing to note about these three pieces is that their control zones can be defined by a specific finite set of integer offsets from the location of the piece itself. The same cannot be said for the other three pieces (Rook, Bishop, Queen), as their Control Zones are not defined by a fixed set of offsets, but a set of directions on the board, by which they can attack (again, assuming that there are no other pieces blocking the way).

The Control Zone directions for the Rook, Bishop and Queen are shown below.

 

 

 

 

 

 

As we begin to work with the infinite boards we will see that this difference between the two sets of pieces profoundly affects how “dense” they can be.

In particular, on infinite boards the control zones of the Rook, Bishop and Queen are also infinite.

Chess Positions

A lot of the definitions below are just stuff I made up. If they correspond to standard chess terms I will mark them with (standard). If I feel that the definition may not be clear, I will give an example as well.

DEFINITION: For a given board $B$ and any subset $\Omega \subseteq B$, a chess position $\Phi$ on $\Omega$ is simply a function $\Phi$ that for each location $x \in \Omega$ there is a piece $p \in \mathscr{P}$ given by $p = \Phi(x)$ at that location. That is, it is a function

$$\Phi: \Omega \rightarrow \mathscr{P}$$

For all of the chess positions we are considering for this puzzle, we only have one kind of piece on the board at the time. And so we will call them “Pawn-positions”, “Queen-positions” etc. Thus if $\Phi$ is a King-position on $\Omega$, then it is a function $\Phi: \Omega \rightarrow \{K, \varnothing\}$.

DEFINITION (standard): A Position is called Unguarded if no piece in the position is in the control zone of another piece. In other words, unguarded positions are positions where the pieces are all “mutually friendly”.

DEFINITION: If $n > 0$ is an integer and $X$ is a (non-empty) chess piece, define $\mathscr{U}(n,X)$ to be the set of all “Maximally Unguarded” X-positions using only piece $X$, on the n-Board. That is, if there are no other unguarded positions with a larger number of pieces.

Measurement of Positions

DEFINITION: For any position $\Phi$ on $\Omega$, we can define the size ($\vert \Phi \vert$) and weight ($\Vert \Phi \Vert$) of that position by the number of elements in its domain $\Omega$ and the number of non-empty locations in its range, ie

$$\vert \Phi \vert = \vert \Omega \vert$$

$$\Vert \Phi \Vert = \vert \{ x \in \Omega: \Phi(x) \neq \varnothing \} \vert$$

EXAMPLE: In the little 4-board below, there are four queens, and the rest are empty.

So, following the defintion above, the board $\Omega$ is the 4×4 board, and its position function $\Phi$ maps every square to the empty piece $\varnothing$ except for the four squares that are mapped to the Queen. The size of the position $\Phi$ is simply the number of squares in $\Omega$, ie $\vert \Phi \vert = \vert \Omega \vert = 16$, while the weight of the position is the number of squares mapped by $\Phi$ to the Queen, ie $\Vert \Phi \Vert$ = 4.

DEFINITION: The for any position $\Phi$ on some board $\Omega$ its Density (denoted $\delta(\Phi)$ ) is the ratio of its weight divided by the size of the position , ie

$$\delta(\Phi) =  \frac{\Vert \Phi \Vert}{ \vert \Phi \vert }$$

DEFINITION: The for any integer n>0, the n-Density (denoted $\delta_n(X)$ ) of a piece $X$ on the n-Board is the maximum density of all possible unguarded positions $\Phi \in \mathscr{U}(n,X)$ ie

$$\delta_n(X) =  \max_{\Phi \in \mathscr{U}(n,X) }\delta(\Phi)$$

EXAMPLE: So, in the previous example for the unguarded queens on the 4-board, it can be seen that:

$$\delta_4(Q) = 4/4^2 = 4/16 = 1/4$$

With all of these preliminaries out of the way, we can now define what we really mean by the density of a piece on an infinite board:

DEFINITION: The Asymptotic Density (denoted $\delta(X)$ ) of a piece $X$ on the infinite board $B_\omega$ is the limit (if it exists) of the n-Density $\delta_n(X)$ of piece X as $n \to \infty$ ie

$$\delta(X) =  \lim_{n \to \infty }\delta_n(X)$$

The Linear Density Measure

For each of the pieces mentioned in the theorem above, their claimed density is of the form $\delta = 1/m$, where $m$ is some positive integer. It turns out that working with density ratios directly is tricky, so we will look at a different “measure” of density that turns out to be easier to work with, as we break a large board into tiles.

So, suppose $w$ is the weight of an X-position $\Phi$ on a set $\Omega$ of size $s$. Then the density $\delta$ is given by

$$\delta = \frac{w}{s}$$

and so if indeed $\delta=1/m$ then

$$1 = m\delta = m\frac{w}{s}$$

and therefore $mw = s$, which is to say that whenever a position has density 1/m, then we can also write

$$mw – s = 0$$

Using this fact, for any sub-position $\Upsilon \subseteq \Phi$ let’s define the “m-linear density” measure function $\Lambda_m(\Upsilon)$ by

$$\Lambda_m(\Upsilon) = m \Vert\Upsilon\Vert  – |\Upsilon|$$

Intuitively, what this measure value tells you is how much over or under the expected density a position is from $1/m$. if the value is exactly zero then the density is exactly $1/m$.  We now present a lemma (ie, a small theorem we can prove now and use later):

LEMMA 1: If $\Phi$ and $\Upsilon$ are two positions defined on disjoint subsets $S$ and $T$ of a board $B_n$, and $m > 0$ is an integer then

$$\Lambda_m(\Phi \cup \Upsilon) = \Lambda_m(\Phi) + \Lambda_m(\Upsilon)$$

that is, the m-linear density of the union of two disjoint positions is the sum of the m-linear densities of each.

PROOF: Follows immediately from the fact that the size of the union of disjoint sets is the sum of the sizes, and regrouping of terms:

$$\Lambda_m(\Phi \cup \Upsilon) = m\Vert\Phi \cup \Upsilon\Vert – \vert\Phi \cup \Upsilon\vert$$

$$=m(\Vert\Phi\Vert + \Vert\Upsilon\Vert) – (\vert\Phi\vert + \vert\Upsilon\vert)$$

and so, regrouping like terms:

$$=(m\Vert\Phi\Vert – \vert\Phi\vert) + (m\Vert\Upsilon\Vert -\vert\Upsilon\vert)$$

$$= \Lambda_m(\Phi) + \Lambda_m(\Upsilon)$$

QED (Quod Erat Demonstrandum = which was to be proved).

$\blacksquare$

LEMMA 2: There exists a positive constant $C > 0$ such that the 2, 2, and 4 linear densities $\Lambda(\Omega)$ of maximal unguarded positions $\Phi$ of Pawns, Knights and Kings on the n-board are bounded by the following expressions:

$$ \forall \Phi \in \mathscr{U}(n,P): 0 \le \Lambda_2(\Phi) <  C * n \tag{2.1} $$

$$ \forall \Phi \in \mathscr{U}(n,N): 0 \le \Lambda_2(\Phi) <  C * n \tag{2.2} $$

$$ \forall \Phi \in \mathscr{U}(n,K): 0 \le \Lambda_4(\Phi) <  C * n \tag{2.3} $$

PROOF: We will start with the formula for the Pawn; the other proofs will be similar. We first note that for the $2 \times 2$ tile $T$ for the Pawn case, the linear density is exactly $\Lambda_2(T) = 2*2 – 4 = 0$. Is it possible to place any more than two “friendly” pawns in the tile $T$? No, because each cell in the first row attacks the diagonal cell in the second row, so you can choose at most one pawn from each “attack pair”. This means that for any unguarded pawn position $\Phi$ on the $2 \times 2$ board, its linear density is bounded by $\Lambda_2(\Phi) \le 0$.

So now what about the 2-linear density for the $n \times n$ board $B_n$? Note that if $n$ is divisible by two we can completely fill up the entire board with these 2-tiles, like this:

Now note that since this n-board (for $n$ = 2k even) is the disjoint union of these $2 \times 2$ tiles $T_1, T_2, …T_{k^2}$, then for any unguarded position $\Phi \in \mathscr{U}(n,P)$, its 2-linear density must be the sum of the densities of these tiles (this follows from Lemma 1) But the positions on those tiles must themselves be unguarded positions, and so for each tile, $\Lambda_2 \le 0$. Therefore, we must have that:

$$\Lambda_2(\Phi) = \Lambda_2(T_1) + … + \Lambda_2(T_{k^2}) \le 0 $$

since all of the terms are known to be $\le 0$. Note that we have also shown that the maximum value of 0 can be attained.

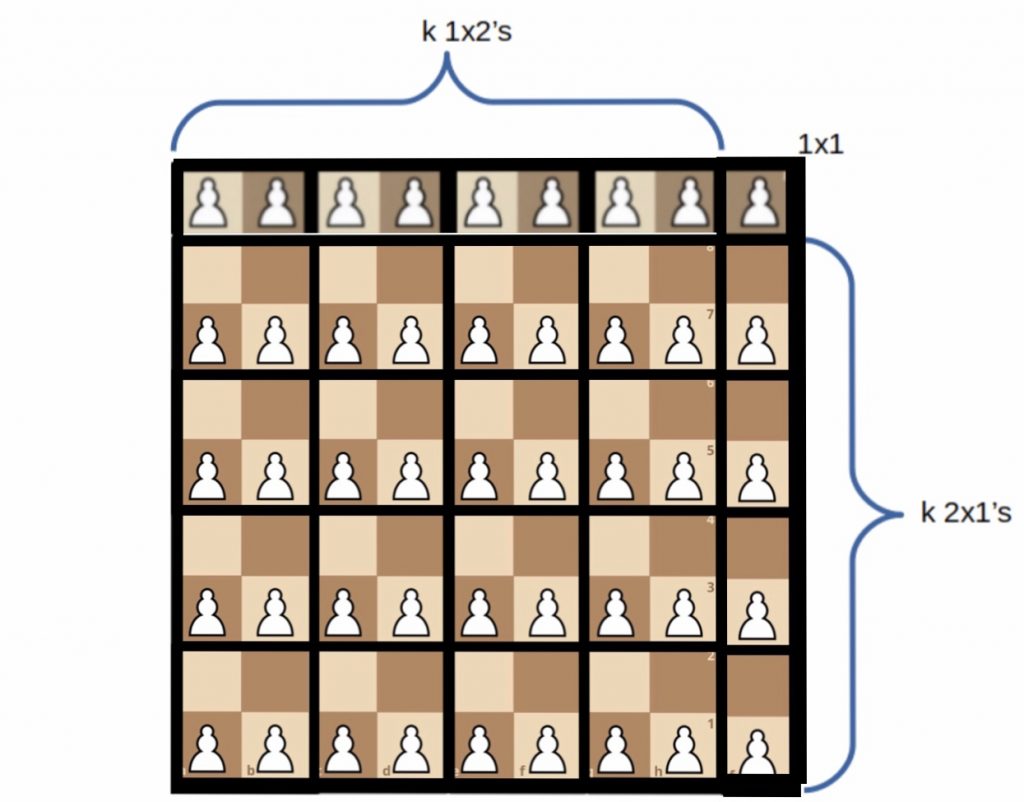
We have just shown that for all even n, and unguarded positions $\Phi$ on the n-board, the value of $\Lambda_2(\Phi)$ is bounded by 0. What about odd n, where $n = 2k+1$? In that case, we can break up the n-board into the disjoint union of $k^2$ tiles which are $2 \times 2$, $k$ tiles which are $1 \times 2$, $k$ tiles which are $2 \times 1$, plus a $1 \times 1$ square, like this:

So now we can play the same game here, and compute the largest possible values of $\Lambda_2$ for each of these little blocks. For both the 1×2 and 2×1 tiles, we have no attack-pairs, and so we can fill both squares with pawns, giving them a maximal 2-density of $\Lambda_2 = 2*2 -2 = 2$. Similarly, we can fill the single 1×1 square with a pawn, for a 2-density of $\Lambda_2 = 2*1 -1 = 1$.

Now there are $k$ of each of the 1×2’s and 2×1’s, and $k^2$ of the 2×2’s and so altogether we can bound the 2-density of the odd n-Board by the sum of these bounds, ie

$$\Lambda_2(\Phi) = k^2 \Lambda_2(2×2) + k\Lambda_2(1×2) + k\Lambda_2(2×1) + \Lambda_2(1×1)$$

$$ \le k^2*0 + k * 2  + k * 2 + 1 $$

$$ \le 4k + 1 \le 4k + 2 $$

$$ \le 2 * (2k + 1) \le 2n $$

And so, what all this means is that for the Pawns, given any unguarded position $\Phi$ on any n-Board, we can bound the largest possible value for its 2-density with a value of C=2, ie,  $\Lambda_2(\Phi) \le 2n$. This proves part (2.1).

Similarly, for the King, we can play the same game, but now using the 4-density $\Lambda_4$. In this case, we can only place one king on the 2×2 tile (since each corner attacks all the others, forming an “attack quadruple”). This gives the 2×2 tile the maximal 4-density of $\Lambda_4 = 4*1 – 4 = 0$. And in the same way, we can show that for even n, the 4-density is bounded by 0, and for the odd case where $n=2k+1$, we can place one king each on the 1×2 and 2×1’s (for a density of $4*1 – 2 = 2$), and one king on the single cell (for a density of $4*1 -1 = 3$). Putting it all together, the King’s 4-density on the odd n-board is given by

$$\Lambda_4(\Phi) = k^2 \Lambda_4(2×2) + k\Lambda_4(1×2) + k\Lambda_4(2×1) + \Lambda_4(1×1)$$

$$ \le k^2*0 + k * 2  + k * 2 + 3 $$

$$ \le 4k + 3 \le 6k + 3 $$

$$ \le 3 * (2k + 1) \le 3n $$

And so for the King we can use the constant $C=3$, so $\Lambda(\Phi) \le 3n$.  This proves (2.3).

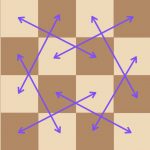
Finally, for the Knight, we have to work a bit harder. The Control Area around the knight extends beyond just a single square, and so we need to use a 4×4 tile to build up a solution. In the 4×4 tile we showed above, we were able to fill exactly half (8) with friendly knights, giving the 4×4 tile a 2-density of $\Lambda_2 = 2*8 – 16 = 0$, just like the Pawn. To prove that this is the best we can do with the 4×4 tile and knights, consider the following “attack pairs” of knights on the tile:

We see that there are eight pairs of mutually-attacking squares by knight moves, meaning we can choose at most one from each pair on which to put a knight. This means there can be at most eight friendly knights on any 4×4 tile. And so, just as with pawns we have $\Lambda_2 \le 0$ on any 4×4 tile.

By the same arguments we gave before, if $n$ is divisible by 4, then we can show that an unguarded knight position on an n-board has density $\Lambda_2 \le 0$, and for all other $n = 4j + k$, with $k \le 3$, we can cover the n-board by $j^2$ 4×4 tiles, $2j$ tiles on the border of size $k \times 4$, which can be shown to never have 2-linear densities greater than $\Lambda_2 = 4$, plus a $k \times k$ corner tile, with density no greater than 1. Putting this altogether, it can be shown that a value of $C=1$ is good enough for knights to bound $\Lambda_2(\Phi) \le C*n$ for any unguarded $\Phi \in \mathscr{U}(n, N)$. This proves inequality (2.2) and the Lemma.

$\blacksquare$

PROOF OF THEOREM 1

The theorem is in three parts, for the Pawn, Knight, and King. We will only show the proof for the Pawn, the other proofs are identical in structure. From Lemma 2, formula (2.1), there is a positive constant C such that for all positive integers $n$ and maximally unguarded Pawn positions $\Phi$ on the n-Board, we have

$$ 0 \le \Lambda_2(\Phi) <  C * n$$

which by definition of $\Lambda_2$ means that

$$ 0 \le 2*\Vert \Phi \Vert – \vert \Phi \vert < C*n $$

Dividing both sides by $\vert \Phi \vert$ we have

$$  0 \le \frac{2*\Vert \Phi \Vert}{\vert \Phi \vert} – 1 < \frac{C*n}{\vert \Phi \vert}$$

But since on the n-Board $\vert \Phi \vert = n^2$, we can use the definition of the position density $\delta(\Phi)$ to obtain

$$ 0\le 2\delta(\Phi) – 1 < C/n$$

in other words (adding one and dividing by 2):

$$ \frac{1}{2} \le \delta(\Phi) < \frac{1}{2} + C/2n$$

And so, since $C$ is a positive constant, as $n$ goes to infinity, the value of $C/2n$ becomes vanishingly small, and in the limit goes to zero. By the definition of the asymptotic density, then, the value of $\delta(Pawn)$ is exactly 1/2, which was to be proved.

$\blacksquare$

Unguarded Positions on the Infinite Board

So far, we have been talking about the density of unguarded positions on large but finite boards $B_n$, and their limit as $n \to \infty$ (“n goes to infinity”). But what happens when $n$ gets there? Is there a position on the infinite board $B_\omega$ that is still “unguarded”, and what do we mean by “maximal”?

If we use the finite solutions as a guide, we can quickly propose positions $\Phi_p$ on $B_\omega$ for p = Pawn, Knight, and King. Recall that a “position” on any board B is simply a function mapping every element $(x,y) \in B$ to a member of $\mathscr{P}$, the set of all chess pieces including the “empty” piece $\varnothing$. The omega board consists of all integer pairs $(x,y)$ such that x and y are greater than or equal to zero (so, the bottom left corner square is $(0,0)$).

The solutions are:

$$\Phi_P(x,y)=
\begin{cases}
P, & \text{if $y$ is even} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{Pawn}
$$

 

$$\Phi_N(x,y)=
\begin{cases}
N, & \text{if $(x+y)$ is even} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{Knight}
$$

 

$$\Phi_K(x,y)=
\begin{cases}
K, & \text{if $x$ is even AND $y$ is even} \\
\varnothing, & \text{otherwise}
\end{cases}\tag{King}
$$

It is relatively straightforward to see that when restricted to a finite n-Board these positions are the same as the ones using the “tiles” we defined above, and so they are still unguarded positions. But in what sense are they “maximal”? The weight of these positions are infinite, so how can one infinite position have a greater weight than another? The answer is, they are maximal in that expanding the position to include additional pieces in locations where the original position does not, must also have a hostile piece in the set.

The proof that these positions are indeed maximal, is left as an exercise to the reader.

What the infinite solutions look like

Here are the Knight and King Positions for the infinite boards, as viewed from a great distance (the white squares are the empty ones):

 

 

 

 

 

 

 

 

 

 

This is not actually an infinite board, of course, but a 300 x 300 one. As you can see, as the number of squares on a side increases to infinity, the individual pieces blur out to form a shade of grey, about 50% black for the Knight, and 25% black for the King. Another way to define the density, is that if you were to throw a dart at one of the boards (say, the King), the odds would be 1/4 that your dart would hit a King.

In the next post, we will look at the Bishops, Rooks, and Queens, and see just how strange and different the situation becomes, especially as we venture into larger transfinite boards.