On Leadership and the President as CEO

Editor Comment: I wrote this piece as a draft way back in 2012, during which time the Presidential CEO contender was Mitt Romney, and some had advocated for him (as for Ross Perot) because of his business experience. I never published this piece then, but the words seem even more salient, now that we are in this dubious boat. I therefore present and publish it today, in its original form. You be the judge. -NR
There has been some discussion in the course of the recent [2012] presidential campaign, with the general implication being that the President of the United states is (or should be evaluated as) the CEO of the country, and at any rate must provide leadership in how the country is run.
We are all story tellers. And the archetype of a “Leader” is a profound story, and not always a healthy one in a civilized world. In another essay, I hope sometime to discuss the two metaphorical and psychological ways I observe groups of people organize themselves and others, called Vertical (top-dog, hierarchical, canine, Yang), and Horizontal (egalitarian, all equal, “it takes a village”, feline, Yin). A Leader is a character in the “Vertical” view of the world. I’m not saying either view is entirely good, but each has its hazards.
I tend to agree with the founders of this country who had grown sick of Old World countries that were “run” by somebody, whether their name be King George or Putin or Berlusconi…or Obama if power ever goes to his head. Regardless of how my philosophy has evolved, to this day I remain a profound admirer of Ayn Rand, whose supreme heroes John Galt and Hank Rearden were brilliant, rational and secular men who did not seek leaders and did not seek to be a leader — and all they asked of the government was for it to Get The Hell Out of Their Way and let them pursue their work and happiness, to the best of their ability.
Galt and Rearden are heroes for (as Obama recently said in Rolling Stone) smart 17 year old intravert misfit teenagers, who feel the world does not understand them. And remain so for those who grow up to be smart adult emotionally integrated intravert misfits who name their houses “Anthem” for more reason than one.
Regarding CEO’s, an article from Thomson Reuters’s archives indicates that the three top skills for an entrepreneurial CEO are:
- Financial Management
- Communication
- Motivation of Others
Good god, I must waste half my time at work convincing whoever is my current boss not to promote me to some “leadership” or “management” role involving people skills and such. Communication I can handle, preferably by email and preferably from far away here in Zion Canyon; if they really want eye-contact we can Skype. I’m Scotty in the engine room and dilithium crystals are fragile, let Kirk deal with the damn aliens. I have no interest in learning motivational psychology or finance professionally. But I know myself. I remain a shy but bright mathematician and software architect, who solves difficult problems in the structure of programs and languages that make it possible for those who write the higher-level business logic to express it coherently, and execute it fast and effectively. For me to be promoted to an executive or managerial role would be tragic for all involved, and I state as much explicitly in my annual employee performance review. Just get the hell out of my way and let me do work that makes me happy and makes you a profit. Everybody wins!
The genius of our country is that it was the first on the planet to be designed based on principles, predicated on the idea that its purpose was to establish ground rules preserving the rights of man, and as men are prone to abrogate power, the founders split the government and its powers into three separate branches. Of these three, only congress is charged with the formulation and passage of laws and its leadership role is composed of many men and women to prevent a single ambitious man dominating. The executive branch was originally intended to be purely executive and the president was intentionally weak, and though he has veto power, certainly not a leadership role. Indeed, George Washington refused proposals that he be made King.
The “leaders” of our country were always reluctant ones, and rightfully so.
Alas, as time has passed, the nature of humanity seems to be that some segment who leans toward “The Vertical” will always seek a strong powerful figurehead to guide them and save them, whether in the form of an all powerful deity, or as a testosterone laden bully/hero such as Mussolini or Stalin (or even FDR, when he tried to pack the Supreme Court). And unfortunately, with a strong powerful leader, you also wind up with a large, powerful government.
I still agree with fiscal conservatives that the proportion of GDP consumed by the current government is far too large, and poses an existential threat to the country. One place of many where I disagree with Ayn Rand and Libertarians now is on the minimal “ground rules” established by a morally defensible government: For example, I would expand the Libertarian “national defense” segment to include defense against natural disasters and disease, from which an argument for a universal baseline healthcare system can be derived, and by my thinking should come directly out of the Defense Budget.
Getting back to leadership, I can only think of a few times where the person in the role of the President has stood up and used the “bully pulpit” to deliver helpful words crafted in thought and grace, to speak to the American people in a way that either united them all as a people, or brought a modicum of closure. FDR’s fireside chats, JFK’s moon speech, and yes Reagan’s address following the Challenger disaster. But there were others such as Martin Luther King Jr, who also served that role, armed only with the power of their own spiritual substance and the confidence in their cause, with no need of elected office.
If we are talking about the president leading the country by putting in place dramatic changes in the economic and regulator power of the state as well as its size, then there are only a few examples of this, one with FDR (who dramatically increased the size and scope) and Reagan (who dramatically decreased it). As president, however, both remained powerless to implement their goal without the fact that congress also had to be in the same party in order to propose and pass those laws, as well as approve members of the Supreme Court to interpret and not strike down those laws. In general, however, it has been observed that Americans seem to be more comfortable when the two branches that pass and sign bills are split. Americans don’t seem to care so much who is in which branch, just so long as they are at odds, in line with the “checks and balances” concept.
We are Americans, where each person is the owner of their own destiny, and who seem to mistrust any one man or party to claim power over them, even if we may agree with them. The president’s activities by rights and by the founder’s intent should be as much in the daily news as the day to day activities of the school janitor. The fact that some have come to seek a President to act as a a leader and CEO of the country is a disturbing state of affairs, in my opinion.

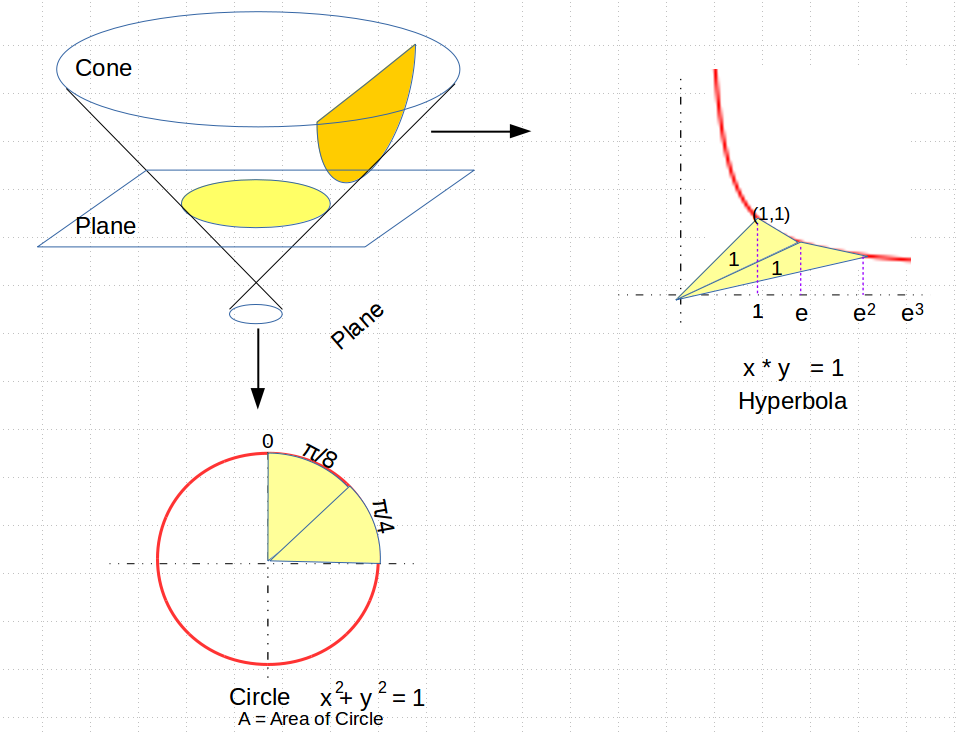
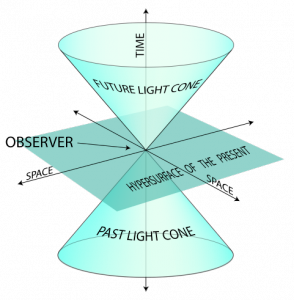

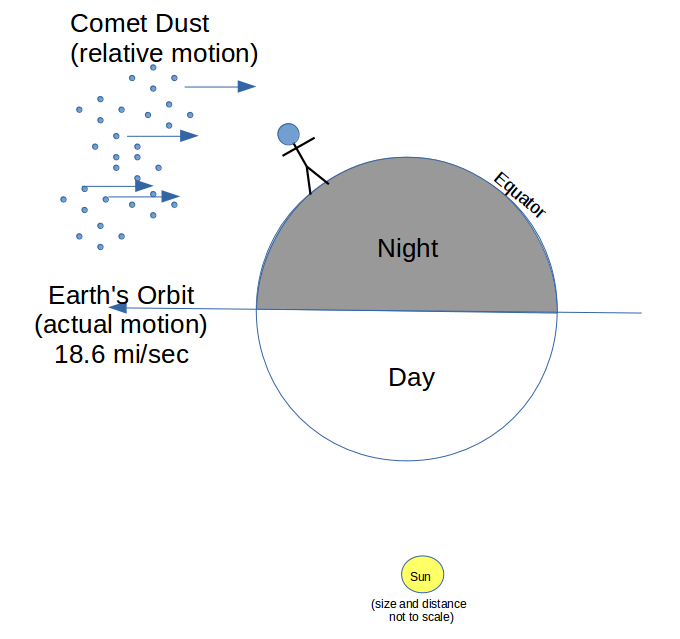
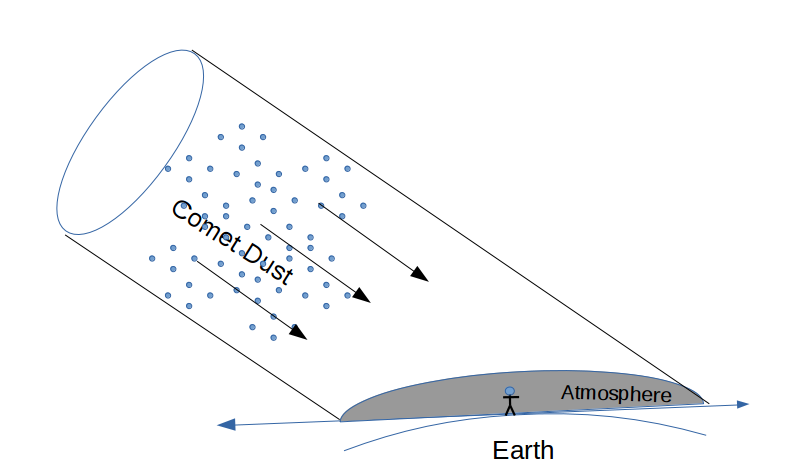
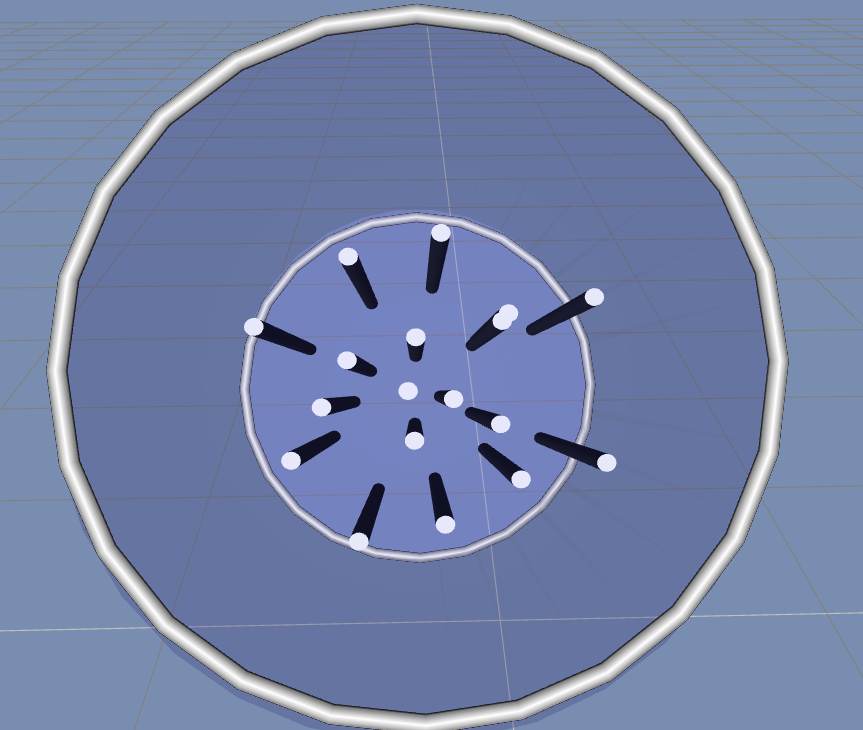
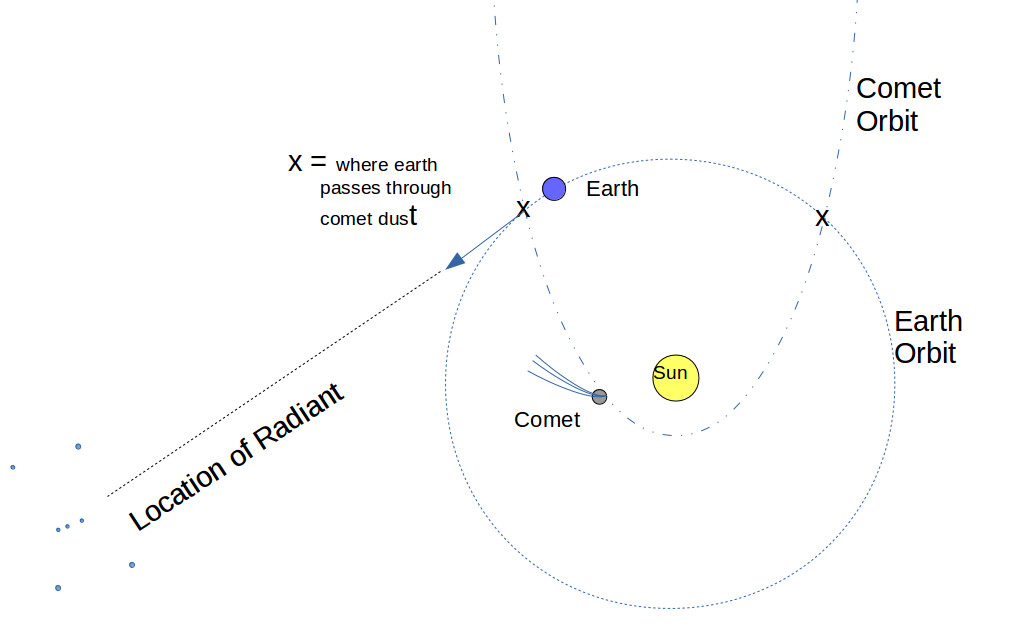



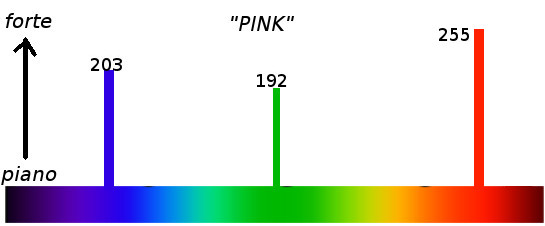


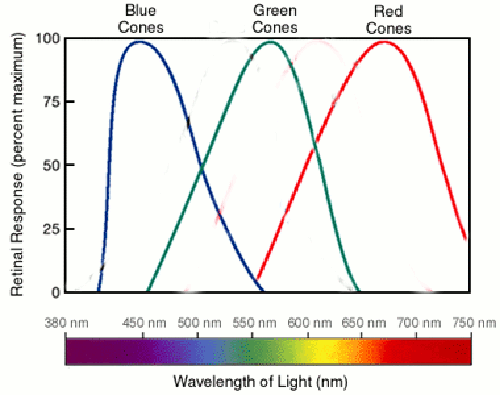






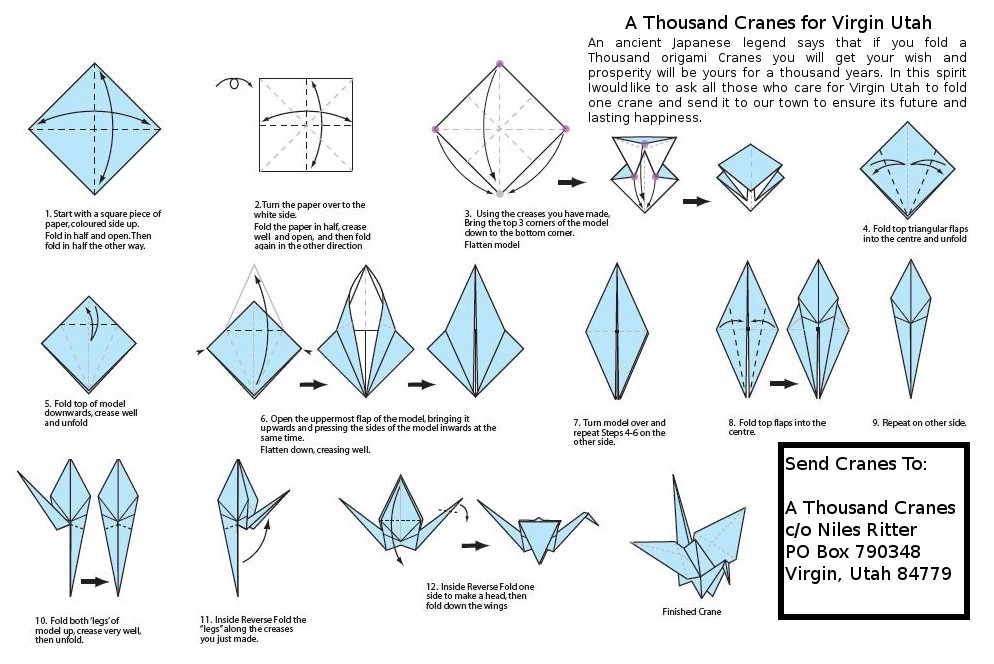




 (aleph-null), which would count all of them at once. Some called this infinity, but it is really just aleph, another number.
(aleph-null), which would count all of them at once. Some called this infinity, but it is really just aleph, another number.



 highly energetic border collie mix, a herder breed, who by her nature needs to be walked several times a day, given her shots, kept active and busy or she will eat and destroy your plants, shoes, blankets etc, and needs to be trained not to herd your other pets and kids. You need to be aware of all of this before you give your kids the cute little puppy, so that later you don’t renege on your promise and one day in frustration drive the dog out to a lonely stretch of highway in the southwest Utah desert, and abandon it on the road to be killed by cars or coyotes. If you do such a thing you also abandon your right to be called a Human(e) being. Only if the animal is very lucky, will she find a home occupied by people who take responsibility for the creatures entrusted to them, because they know there is no such word as Have.
highly energetic border collie mix, a herder breed, who by her nature needs to be walked several times a day, given her shots, kept active and busy or she will eat and destroy your plants, shoes, blankets etc, and needs to be trained not to herd your other pets and kids. You need to be aware of all of this before you give your kids the cute little puppy, so that later you don’t renege on your promise and one day in frustration drive the dog out to a lonely stretch of highway in the southwest Utah desert, and abandon it on the road to be killed by cars or coyotes. If you do such a thing you also abandon your right to be called a Human(e) being. Only if the animal is very lucky, will she find a home occupied by people who take responsibility for the creatures entrusted to them, because they know there is no such word as Have.

